题目内容
16.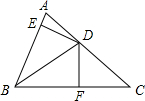 如图,BD是∠ABC的平分线,DE⊥AB,DF⊥AB垂足为E,S△ABC=60cm2,AB=9cm,BC=15cm,则DE的长是5.
如图,BD是∠ABC的平分线,DE⊥AB,DF⊥AB垂足为E,S△ABC=60cm2,AB=9cm,BC=15cm,则DE的长是5.
分析 先根据角平分线的性质得出DE=DF,再由三角形的面积公式即可得出结论.
解答 解:∵如图,BD是∠ABC的平分线,DE⊥AB,垂足为点E,DF⊥BC,垂足为F,
∴DE=DF.
∵S△ABC=60,AB=9,BC=15,
∴S△ABD+S△BCD=$\frac{1}{2}$AB•DE+$\frac{1}{2}$BC•DF=60,
即$\frac{1}{2}$×9•DE+$\frac{1}{2}$×15•DE=60,
解得DE=5.
故答案为:5.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.若方程组$\left\{\begin{array}{l}{3x-4y=-1}\\{2x+3my=-\frac{2}{3}}\end{array}\right.$仅有一组解,则m的取值是( )
| A. | m可以取任何实数 | B. | m≠$\frac{8}{9}$ | C. | m≠-$\frac{8}{9}$ | D. | 以上均不对 |
 如图,已知BC=DC,需要再添加一个条件∠ACB=∠ACD或AB=AD可得△ABC≌△ADC.
如图,已知BC=DC,需要再添加一个条件∠ACB=∠ACD或AB=AD可得△ABC≌△ADC. 如图,A、C两乡镇到水渠边l的距离分别为AB=2km,CD=4km,且BD=8km.
如图,A、C两乡镇到水渠边l的距离分别为AB=2km,CD=4km,且BD=8km.
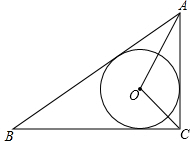 如图所示,⊙O内切于△ABC,若∠ACB=90°,∠AOC=105°,AB=$\frac{8}{3}$,求AC及S△ABC.
如图所示,⊙O内切于△ABC,若∠ACB=90°,∠AOC=105°,AB=$\frac{8}{3}$,求AC及S△ABC.