题目内容
4. 如图,A、C两乡镇到水渠边l的距离分别为AB=2km,CD=4km,且BD=8km.
如图,A、C两乡镇到水渠边l的距离分别为AB=2km,CD=4km,且BD=8km.(1)在水渠边l上要建一个水电站P,使得PA+PC最小,请在图中画出P的位置(保留作图痕迹),不必说明理由.
(2)求出PA+PC最小值.
分析 (1)作点A关于直线l的对称点A′,连接A′C交l于点P,则P点即为所求点;
(2)过A′作A′E⊥CD,交CD的延长线于E,再根据勾股定理即可得出A′C的长.
解答 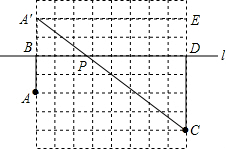 解:(1)如图;
解:(1)如图;
(2)由作图可得最短路程为A′C的距离,
过A′作A′E⊥CD,交CD的延长线于E,
则DE=A′B=AB=2km,A′E=BD=8km,CE=2+4=6km,
根据勾股定理可得,A′C=$\sqrt{A′{E}^{2}+C{E}^{2}}$=10km.
即PA+PC最小值为10km.
点评 本题考查的是轴对称-最短路线问题,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
14.下列各组图形中一定相似的是( )
| A. | 各有一个角为40°的两等腰三角形 | |
| B. | 有两边之比都为2:3的两直角三角形 | |
| C. | 有两边及其中一边上的高对应成比例的两三角形 | |
| D. | 两边及两边夹角的平分线对应成比例的两三角形 |
 如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.
如图,反比例函数y=$\frac{18}{x}$的图象过矩形OABC的顶点B,OA、OC分别在x轴、y轴的正半轴上,OA;OC=1:2,矩形OABC的对角线交于点E.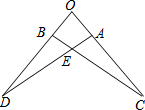 如图,△OAD≌△OBC,且∠O=80°,∠C=20°,则∠AEB=120°.
如图,△OAD≌△OBC,且∠O=80°,∠C=20°,则∠AEB=120°.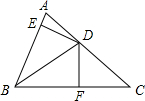 如图,BD是∠ABC的平分线,DE⊥AB,DF⊥AB垂足为E,S△ABC=60cm2,AB=9cm,BC=15cm,则DE的长是5.
如图,BD是∠ABC的平分线,DE⊥AB,DF⊥AB垂足为E,S△ABC=60cm2,AB=9cm,BC=15cm,则DE的长是5.