题目内容
在平面直角坐标系中，已知点A（0，2）、B（4，1），点P在x轴上，则PA+PB的最小值是 ．
考点：轴对称-最短路线问题,坐标与图形性质
专题：
分析：求出A点关于x轴的对称点A′，连接A′B，交x轴于点P，则P即为所求点，利用两点间的距离公式即可求解．
解答：
解：作点A关于x轴的对称点A′，连接A′BA交x轴于点P，则P即为所求点；
∵点A（0，2），
∴点A关于x轴的对称点A′的坐标为（0，-2），
∵A′（0，-2），B（4，1），
∴A′B=
=5．
即PA+PB的最小值为5．
故答案为5．
解：作点A关于x轴的对称点A′，连接A′BA交x轴于点P，则P即为所求点；∵点A（0，2），
∴点A关于x轴的对称点A′的坐标为（0，-2），
∵A′（0，-2），B（4，1），
∴A′B=
| (0-4)2+(-2-1)2 |
即PA+PB的最小值为5．
故答案为5．
点评：本题考查的是最短线路问题及两点间的距离公式，解答此题的关键是熟知两点之间线段最短的知识．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC分别交DE、BE于点G、H，则∠EFC=
作图题：
如图，小明沿着某斜坡向上行走了13m后，他的相对位置升高了5m，如果他沿着该斜坡行走了26米，那么他的相对位置升高了
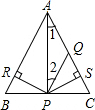如图，△ABC中，∠1=∠2，PR=PS，PR⊥AB于R，PS⊥AC于S，则下列三个结论：①AS=AR；②QP∥AB；③△BRP≌△QSP，（ ）| A、全部正确 | B、①和②正确 |
| C、仅①正确 | D、①和③正确 |
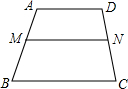如图，在梯形ABCD中AD∥BC，点M为腰AB上的一点，MN∥BC交DC于点N，MN与AD是否平行？请说明理由，分别测量出点MN到BC的距离，两者有何关系．