题目内容
 如图,△ABC内接于⊙O,AB=AC,∠BAC=120°,BD为⊙O的直径.求证:AC∥BD.
如图,△ABC内接于⊙O,AB=AC,∠BAC=120°,BD为⊙O的直径.求证:AC∥BD.考点:圆周角定理
专题:
分析:如图,证明∠ACB=30°;证明∠DBC=30°,得到∠DBC=∠ACB,即可解决问题.
解答: 证明:∵AB=AC,∠BAC=120°,
证明:∵AB=AC,∠BAC=120°,
∴∠ACB=∠ABC=
=30°;
∵BD为⊙O的直径,∠BAC=120°,
∴∠DAC=120°-90°=30°,
∴∠DBC=∠DAC=30°;
∴∠DBC=∠ACB,
∴AC∥BD.
 证明:∵AB=AC,∠BAC=120°,
证明:∵AB=AC,∠BAC=120°,∴∠ACB=∠ABC=
| 180°-120° |
| 2 |
∵BD为⊙O的直径,∠BAC=120°,
∴∠DAC=120°-90°=30°,
∴∠DBC=∠DAC=30°;
∴∠DBC=∠ACB,
∴AC∥BD.
点评:该题主要考查了圆周角定理及其推论、等腰三角形的性质、平行线的判定等几何知识点的应用问题;牢固掌握定理是基础,灵活运用解题是关键.

练习册系列答案
相关题目
 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、丽 | C、淮 | D、南 |
和一个已知点P的距离等于3cm的直线可以画( )
| A、1条 | B、2条 | C、3条 | D、无数条 |
 已知如图,直线y=-
已知如图,直线y=- 如图,是一个圆锥形粮仓顶盖,底面半径为5m,圆锥的高为5
如图,是一个圆锥形粮仓顶盖,底面半径为5m,圆锥的高为5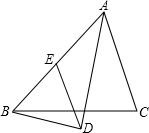 在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC交AB于E.
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC交AB于E.