题目内容
 已知如图,直线y=-
已知如图,直线y=-| 3 |
| ||
| 3 |
(1)求点P的坐标;
(2)求S△OPA的值;
(3)动点E从原点O出发,沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,F的坐标为(a,0),矩形EBOF与△OPA重叠部分的面积为S.求:S与a之间的函数关系式.
考点:一次函数综合题
专题:综合题
分析:(1)联立两直线解析式,求出交点P坐标即可;
(2)由A的坐标确定出OA的长,由OA乘以P纵坐标求出三角形AOP面积即可;
(3)由F坐标确定出OF的长,得到E的横坐标为a,代入直线OP解析式表示出E纵坐标,即为EF的长,分三种情况考虑:当0<a≤
时,矩形EBOF与三角形OPA重叠部分为直角三角形OEF,表示出三角形OEF面积S与a的函数关系式;当
<a≤
时,重合部分为直角三角形与梯形面积之和,求出S与a函数关系式;当a>
时,重合面积为三角形OPA面积,求出S与a函数关系式即可.
(2)由A的坐标确定出OA的长,由OA乘以P纵坐标求出三角形AOP面积即可;
(3)由F坐标确定出OF的长,得到E的横坐标为a,代入直线OP解析式表示出E纵坐标,即为EF的长,分三种情况考虑:当0<a≤
| 3 |
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
解答:解:(1)联立得:
,
消去y得:-
x+4=
x,即x=
,
将x=
代入得:y=1,
则P坐标为(
,1);
(2)由直线y=-
x+4,令y=0,得到x=
,即A(
,0),
则S△OPA=
OA•P纵坐标=
×
×1=
;
(3)分三种情况考虑:
当0<a≤
时,由F坐标为(a,0),得到OF=a,
把E横坐标为a,代入y=
x,得:y=
a,即EF=
a,
此时S=
OF•EF=
a2(0<a≤
);
当
<a≤
时,S=
×1×
+
(a-
)(
a+1)=
+
(
a2+a-a-
)=
a2(
<a≤
);
当a>
时,矩形EBOF与△OPA重叠部分的面积为S=S△OPA=
OA•P纵坐标=
×
×1=
.
|
消去y得:-
| 3 |
| ||
| 3 |
| 3 |
将x=
| 3 |
则P坐标为(
| 3 |
(2)由直线y=-
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
则S△OPA=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
(3)分三种情况考虑:
当0<a≤
| 3 |
把E横坐标为a,代入y=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
此时S=
| 1 |
| 2 |
| ||
| 6 |
| 3 |
当
| 3 |
4
| ||
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| ||
| 6 |
| 3 |
4
| ||
| 3 |
当a>
4
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
2
| ||
| 3 |
点评:此题属于一次函数综合题,涉及的知识有:两直线的交点坐标,坐标与图形性质,利用了分类讨论的思想,弄清题意是解本题的关键.

练习册系列答案
相关题目
 如图,已知线段b、c、m,求作△ABC,使它的两边分别等于b和c,第三边上的中线等于m.
如图,已知线段b、c、m,求作△ABC,使它的两边分别等于b和c,第三边上的中线等于m.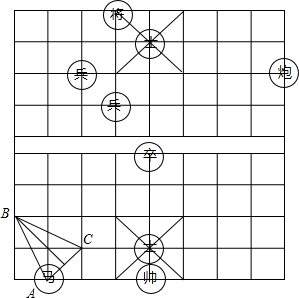 亲爱的同学,你会玩中国象棋吗?如图所示的一盘象棋中.马走的两步棋从A到B再到C,若小正方形边长为1,求B到AC的距离.
亲爱的同学,你会玩中国象棋吗?如图所示的一盘象棋中.马走的两步棋从A到B再到C,若小正方形边长为1,求B到AC的距离. 如图,△ABC内接于⊙O,AB=AC,∠BAC=120°,BD为⊙O的直径.求证:AC∥BD.
如图,△ABC内接于⊙O,AB=AC,∠BAC=120°,BD为⊙O的直径.求证:AC∥BD.