题目内容
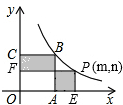 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=| k |
| x |
| k |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:利用正方形的性质得OA=AB=2,则B点坐标为(2,2);把B(2,2)代入y=
中,即可求出k;P(m,n)在y=
上,得到mn=4,S=AE•PE+CB•CF=(m-2)•n+2(2-n)=mn-2n+4-2n=mn-4n+4=8-
,根据S>1,可得出m的取值范围.
| k |
| x |
| k |
| x |
| 16 |
| m |
解答:解:∵正方形OABC的面积为4,
∴OA=AB=2,
∴B点坐标为(2,2);
∵点B在函数y=
(x>0,k>0)的图象上,
∴把B(2,2)代入y=
中,
得k=4;
∴反比例函数的解析式为y=
;
∵P(m,n)在y=
上,∴mn=4,∴n=
,
∵S=AE•PE+CB•CF,
∴S=(m-2)•n+2(2-n)=mn-2n+4-2n=mn-4n+4=8-
,
∵S>1,
∴
<7,
∵x>0,
∴m的取值范围m>
.
∴OA=AB=2,
∴B点坐标为(2,2);
∵点B在函数y=
| k |
| x |
∴把B(2,2)代入y=
| k |
| x |
得k=4;
∴反比例函数的解析式为y=
| 4 |
| x |
∵P(m,n)在y=
| 4 |
| x |
| 4 |
| m |
∵S=AE•PE+CB•CF,
∴S=(m-2)•n+2(2-n)=mn-2n+4-2n=mn-4n+4=8-
| 16 |
| m |
∵S>1,
∴
| 16 |
| m |
∵x>0,
∴m的取值范围m>
| 16 |
| 7 |
点评:本题考查了反比例函数系数k的几何意义,先利用待定系数法确定反比例的解析式,那么图象上所有点的横纵坐标的乘积为定值.也考查了矩形的性质以及分类讨论思想的运用.

练习册系列答案
相关题目
延长线段AB到C,下列说法正确的是( )
| A、点C在线段AB上 |
| B、点C在直线AB上 |
| C、点C不在直线AB上 |
| D、点C在直线BA的延长线上 |
下列各组数中,不是“勾股数”的是( )
| A、9,12,15 | ||||
| B、3,5,4 | ||||
C、1,
| ||||
| D、8,17,15 |
 如图,菱形ABCD中,∠B=60°,AB=6cm,点E在AB上,点F在BC上,AE=BF=2cm,连接AF与CE交于P点,求DP的长.
如图,菱形ABCD中,∠B=60°,AB=6cm,点E在AB上,点F在BC上,AE=BF=2cm,连接AF与CE交于P点,求DP的长. 如图,在同一时刻的太阳光下,测出垂直于地面长a m的标杆的影长b m,塔的影长c m,这样就可以计算出该塔的高度了.根据上述方法,你可计算出塔的高度是多少米?
如图,在同一时刻的太阳光下,测出垂直于地面长a m的标杆的影长b m,塔的影长c m,这样就可以计算出该塔的高度了.根据上述方法,你可计算出塔的高度是多少米?