题目内容
 如图,菱形ABCD中,∠B=60°,AB=6cm,点E在AB上,点F在BC上,AE=BF=2cm,连接AF与CE交于P点,求DP的长.
如图,菱形ABCD中,∠B=60°,AB=6cm,点E在AB上,点F在BC上,AE=BF=2cm,连接AF与CE交于P点,求DP的长.考点:菱形的性质
专题:
分析:连接AC,根据菱形的四条边都相等可得AB=BC,然后求出△ABC是等边三角形,根据等边三角形的性质可得∠B=∠CAB=60°,然后利用“边角边”证明△ABF和△CAE全等即可;求出∠BAF=∠ADP,∠DAP=∠AFB,证出△ADP和△BAF全等即可.
解答:解:连接AC,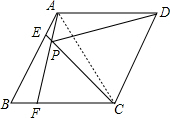
∵四边形ABCD是菱形,
∴AB=BC=AD,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠B=∠CAB=60°,AB=AC=6cm,
∴AD=AC,
在△ABF和△CAE中,
,
∴△ABF≌△CAE(SAS);
∴∠BAF=∠ACE,∠AEC=∠AFB,
∴∠APC=∠AEC+∠BAF=∠AFB+∠BAF=180°-∠B=120°,
∵四边形ABCD是菱形,
∴∠ADC=∠B=60°,
∴∠APC+∠ADC=180°,
∴APCD四点共圆,
∴∠ADP=∠ACE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAP=∠AFB=∠AEC,
在△ADP和△FAB中,
,
∴△ADP≌△FAB,
∴DP=AB=6cm.

∵四边形ABCD是菱形,
∴AB=BC=AD,
∵∠B=60°,
∴△ABC为等边三角形,
∴∠B=∠CAB=60°,AB=AC=6cm,
∴AD=AC,
在△ABF和△CAE中,
|
∴△ABF≌△CAE(SAS);
∴∠BAF=∠ACE,∠AEC=∠AFB,
∴∠APC=∠AEC+∠BAF=∠AFB+∠BAF=180°-∠B=120°,
∵四边形ABCD是菱形,
∴∠ADC=∠B=60°,
∴∠APC+∠ADC=180°,
∴APCD四点共圆,
∴∠ADP=∠ACE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠DAP=∠AFB=∠AEC,
在△ADP和△FAB中,
|
∴△ADP≌△FAB,
∴DP=AB=6cm.
点评:本题考查了菱形的性质,全等三角形的性质和判定,圆内接四边形的性质的应用,解此题的关键是求出△ABF≌△CAE,△ADP≌△FAB,难度偏大.

练习册系列答案
相关题目
 有理数a,b在数轴上的位置如图,则下列各式中正确的是( )
有理数a,b在数轴上的位置如图,则下列各式中正确的是( )| A、a+b<0 | B、a-b<0 |
| C、|b|>a | D、ab<0 |
 如图,CD为⊙O的弦,E、F在直径AB上,EC⊥CD,DF⊥CD.求证:AE=BF.
如图,CD为⊙O的弦,E、F在直径AB上,EC⊥CD,DF⊥CD.求证:AE=BF. 如图,身高1.5m的小明用一个两锐角分别是30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离为5米,求这棵树的高度.(精确到0.1米)
如图,身高1.5m的小明用一个两锐角分别是30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离为5米,求这棵树的高度.(精确到0.1米) 如图所示,把三角形纸片(△ABC)沿DE折叠,当点A落在四边形BCED内部时,请你证明∠1+∠2的值总是个定值.并求出这个定值.
如图所示,把三角形纸片(△ABC)沿DE折叠,当点A落在四边形BCED内部时,请你证明∠1+∠2的值总是个定值.并求出这个定值.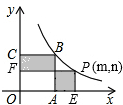 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数