题目内容
 王先生有块地如图所示,已知∠ABC=90°,AB=3米,BC=4米,CD=12米,AD=13米,求这块地的面积多大?
王先生有块地如图所示,已知∠ABC=90°,AB=3米,BC=4米,CD=12米,AD=13米,求这块地的面积多大?考点:勾股定理的逆定理,勾股定理
专题:
分析:连接AC,然后根据勾股定理求出AC的长度,再根据勾股定理逆定理计算出∠ACD=90°,然后根据四边形ABCD的面积=△ABC的面积+△ACD的面积,列式进行计算即可得解.
解答: 解:连接AC,
解:连接AC,
∵∠ABC=90°,AB=3米,BC=4米,
∴AC=
=5,
∵CD=12米,AD=13米,
∴AC2+CD2=52+122=25+144=169,
AD2=132=169,
∴AC2+CD2=AD2,
∴△ACD是∠ACD=90°的直角三角形,
四边形ABCD的面积=△ABC的面积+△ACD的面积
=
AB•BC+
AC•CD
=
×3×4+
×5×12
=6+30
=36(米2).
 解:连接AC,
解:连接AC,∵∠ABC=90°,AB=3米,BC=4米,
∴AC=
| AB2+BC2 |
∵CD=12米,AD=13米,
∴AC2+CD2=52+122=25+144=169,
AD2=132=169,
∴AC2+CD2=AD2,
∴△ACD是∠ACD=90°的直角三角形,
四边形ABCD的面积=△ABC的面积+△ACD的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=6+30
=36(米2).
点评:本题考查了勾股定理,勾股定理逆定理,连接AC,构造出直角三角形是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
如下一排方格中,第1个小方格中的数字是3,第4个小方格中的数字是-1,第7个小方格中的数字是2,其他每个小方格中的字母分别代表一个数,已知任意连续四个小方格中数字的积都等于24,则第2015个小方格中的数字是( )
| 3 | a | b | -1 | c | d | 2 | e | … |
| A、-4 | B、-1 | C、2 | D、3 |
下列命题中,正确的是( )
| A、平面上三个点确定一个圆 |
| B、等弧所对的圆周角相等 |
| C、三角形的外心在三角形的外面 |
| D、与某圆一条半径垂直的直线是该圆的切线 |
 如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么: 用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.
用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.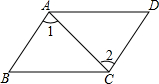 如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?
如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?