题目内容
 如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:
如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,若以M为圆心,r为半径作圆,那么:(1)当直线AB与⊙M相离时,r的取值范围是
(2)当直线AB与⊙M相切时,r的取值范围是
(3)当直线AB与⊙M有公共点时,r的取值范围是
考点:直线与圆的位置关系
专题:
分析:作MN⊥OA于N,如图,根据含30度的直角三角形三边的关系得到MN=
OM=
,然后根据直线与圆的关系得到当r=
时,⊙M与射线OC相切,只有一个公共点;当0<r<
时,⊙M与射线OC相离,没有公共点;当
<r≤5时,⊙M与射线OC有两个公共点,而当r>5时,⊙M与射线OC只有一个公共点.
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
解答:解:作MN⊥OA于N,如图,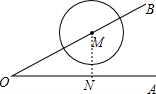
∵∠AOB=30°,
∴MN=
OM=
×5=
,
∴(1)当直线AB与⊙M相离时,r的取值范围是0<r<
;
(2)当直线AB与⊙M相切时,r的取值范围是r=
;
(3)当直线AB与⊙M有公共点时,r的取值范围是r>
.
故答案为:(1)0<r<
(2)r=
(3)r>
.

∵∠AOB=30°,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴(1)当直线AB与⊙M相离时,r的取值范围是0<r<
| 5 |
| 2 |
(2)当直线AB与⊙M相切时,r的取值范围是r=
| 5 |
| 2 |
(3)当直线AB与⊙M有公共点时,r的取值范围是r>
| 5 |
| 2 |
故答案为:(1)0<r<
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
点评:本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d.若直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列几何图形中,对称轴最多的是( )
| A、平行四边形 | B、长方形 |
| C、等边三角形 | D、半圆 |
在
,
,-0.5xy,
,
中,是分式的有( )
| 1 |
| x |
| a2b |
| π |
| a+b |
| 7 |
| x+2 |
| 5+y |
| A、2个 | B、3个 | C、4个 | D、5个 |
 王先生有块地如图所示,已知∠ABC=90°,AB=3米,BC=4米,CD=12米,AD=13米,求这块地的面积多大?
王先生有块地如图所示,已知∠ABC=90°,AB=3米,BC=4米,CD=12米,AD=13米,求这块地的面积多大?