题目内容
解下列一元二次方程:
(1)(x+2)2-25=0(直接开平方法)
(2)2x2-5x-1=0(配方法)
(3)(x+2)2-10(x+2)+25=0(因式分解法)
(4)2x2-7x+3=0(公式法)
(5)x2+2(
-1)x+3-2
=0
(6)(2x-5)2-(x+4)2=0.
(1)(x+2)2-25=0(直接开平方法)
(2)2x2-5x-1=0(配方法)
(3)(x+2)2-10(x+2)+25=0(因式分解法)
(4)2x2-7x+3=0(公式法)
(5)x2+2(
| 2 |
| 2 |
(6)(2x-5)2-(x+4)2=0.
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-配方法,解一元二次方程-公式法
专题:
分析:(1)移项,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)求出b2-4ac的值,再代入公式求出即可;
(5)分解因式,即可得出两个一元一次方程,求出方程的解即可;
(6)分解因式,即可得出两个一元一次方程,求出方程的解即可.
(2)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(3)分解因式,即可得出两个一元一次方程,求出方程的解即可;
(4)求出b2-4ac的值,再代入公式求出即可;
(5)分解因式,即可得出两个一元一次方程,求出方程的解即可;
(6)分解因式,即可得出两个一元一次方程,求出方程的解即可.
解答:解:(1)(x+2)2-25=0,
(x+2)2=25,
x+2=±5,
x1=3,x2=-7;
(2)2x2-5x-1=0,
2x2-5x=1,
x2-
x=
,
x2-
x+(
)2=
+(
)2,
(x-
)2=
,
x-
=
,
x1=
,x2=
;
(3)(x+2)2-10(x+2)+25=0,
(x+2-5)2=0,
x+2-5=0,
x=3,
即x1=x2=3;
(4)2x2-7x+3=0,
b2-4ac=(-7)2-4×2×3=25,
x=
,
x1=3,x2=
;
(5)x2+2(
-1)x+3-2
=0,
(x+
-1)2=0,
x+
-1=0,
x=1-
,
即x1=x2=1-
;
(6)(2x-5)2-(x+4)2=0,
[(2x-5)+(x+4)][(2x-5)-(x+4)]=0,
(2x-5)+(x+4)=0,(2x-5)-(x+4)=0,
x1=
,x2=9.
(x+2)2=25,
x+2=±5,
x1=3,x2=-7;
(2)2x2-5x-1=0,
2x2-5x=1,
x2-
| 5 |
| 2 |
| 1 |
| 2 |
x2-
| 5 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
(x-
| 5 |
| 4 |
| 33 |
| 16 |
x-
| 5 |
| 4 |
| ||
| 4 |
x1=
5+
| ||
| 4 |
5-
| ||
| 4 |
(3)(x+2)2-10(x+2)+25=0,
(x+2-5)2=0,
x+2-5=0,
x=3,
即x1=x2=3;
(4)2x2-7x+3=0,
b2-4ac=(-7)2-4×2×3=25,
x=
7±
| ||
| 2×2 |
x1=3,x2=
| 1 |
| 2 |
(5)x2+2(
| 2 |
| 2 |
(x+
| 2 |
x+
| 2 |
x=1-
| 2 |
即x1=x2=1-
| 2 |
(6)(2x-5)2-(x+4)2=0,
[(2x-5)+(x+4)][(2x-5)-(x+4)]=0,
(2x-5)+(x+4)=0,(2x-5)-(x+4)=0,
x1=
| 1 |
| 3 |
点评:本题考查了解一元二次方程的应用,解此题的关键是能选择适当的方法解一元二次方程,难度适中.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
在
,
,-0.5xy,
,
中,是分式的有( )
| 1 |
| x |
| a2b |
| π |
| a+b |
| 7 |
| x+2 |
| 5+y |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列说法正确的是( )
| A、一个数的平方根一定有两个 |
| B、一个非负数的平方根就是它的算术平方根 |
| C、没有平方根的数一定是负数 |
| D、一个正数的平方根就是它的算术平方根 |
下列命题中,原命题与逆命题不同时成立的是( )
| A、等腰三角形的两个底角相等 |
| B、直角三角形的两个锐角互余 |
| C、对顶角相等 |
| D、线段垂直平分线上的点到线段两端点的距离相等 |
下列分式中是最简分式的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 王先生有块地如图所示,已知∠ABC=90°,AB=3米,BC=4米,CD=12米,AD=13米,求这块地的面积多大?
王先生有块地如图所示,已知∠ABC=90°,AB=3米,BC=4米,CD=12米,AD=13米,求这块地的面积多大?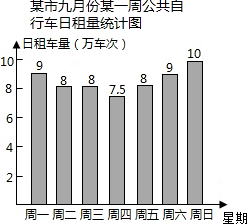 作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对2014年九月份中的7天进行了公共自行车日租车量的统计,结果如图:
作为某市政府民生实事之一的公共自行车建设工作已基本完成,某部门对2014年九月份中的7天进行了公共自行车日租车量的统计,结果如图: