题目内容
5.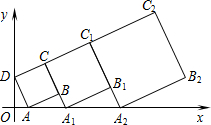 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是( )| A. | 10×($\frac{4}{3}$)4030 | B. | 10×($\frac{4}{3}$)4031 | C. | 10×($\frac{4}{3}$)4032 | D. | 10×($\frac{4}{3}$)4033 |
分析 先求出正方形ABCD的边长和面积,再求出第二个正方形A1B1C1C的面积,得出规律,根据规律即可求出第2016个正方形的面积.
解答 解:∵点A的坐标为(1,0),点D的坐标为(0,3),
∴OA=1,OD=3,
∵∠AOD=90°,
∴AB=AD=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,∠ODA+∠OAD=90°,
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=90°,S正方形ABCD=($\sqrt{10}$)2=10,
∴∠ABA1=90°,∠OAD+∠BAA1=90°,
∴∠ODA=∠BAA1,
∴△ABA1∽△DOA,
∴$\frac{B{A}_{1}}{OA}$=$\frac{AB}{OD}$,即$\frac{B{A}_{1}}{1}$=$\frac{\sqrt{10}}{3}$,
∴BA1=$\frac{\sqrt{10}}{3}$,
∴CA1=$\sqrt{10}$+$\frac{\sqrt{10}}{3}$=$\frac{4\sqrt{10}}{3}$,
∴正方形A1B1C1C的面积=($\frac{4\sqrt{10}}{3}$)2=10×($\frac{4}{3}$)2,…,第n个正方形的面积为10×($\frac{4}{3}$)2n
∴第2016个正方形的面积为10×($\frac{4}{3}$)4032;
故选C.
点评 本题考查了正方形的性质以及坐标与图形性质;通过求出正方形ABCD和正方形A1B1C1C的面积得出规律是解决问题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
11.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )


| A. | ($\frac{1}{2}$)2014 | B. | ($\frac{1}{2}$)2015 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2017 |
15.-3的负倒数( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |

 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).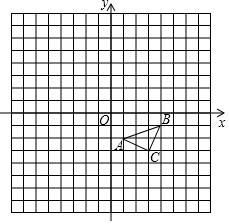 如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).
如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).