题目内容
14.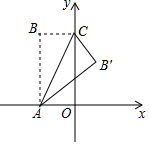 如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
分析 作B′E⊥x轴,设OD=x,在Rt△AOD中,根据勾股定理列方程,可求得D点的坐标,然后依据△ADO∽△AB′E可求得B′E、AE的长,从而可求得点B′的坐标.
解答 解:作B′E⊥x轴,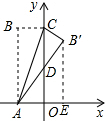
∵∠BAC=∠B′AC,∠BAC=∠OCA,
∴∠B′AC=∠OCA,
∴AD=CD,
设OD=x,AD=4-x,
在Rt△AOD中,根据勾股定理列方程得:22+x2=(4-x)2,
解得:x=1.5,
∴OD=1.5.
∴AD=CD=4-1.5=2.5.
∵CO⊥AO,B′E⊥AO,
∴DO∥B′E.
∴△ADO∽△AB′E.
∴$\frac{AD}{AB′}$=$\frac{OD}{B′E}$=$\frac{AO}{AE}$,即$\frac{2.5}{4}$=$\frac{1.5}{B'E}$=$\frac{2}{AE}$.
解得:B′E=$\frac{12}{5}$,AE=$\frac{16}{5}$.
∴OE=$\frac{16}{5}$-2=$\frac{6}{5}$
∴点B′的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
故答案为:($\frac{6}{5}$,$\frac{12}{5}$).
点评 本题主要考查的是翻折的性质、勾股定理的应用、相似三角形的性质和判定,求得点D的坐标是解题的关键.

练习册系列答案
相关题目
2.下列运算:①x2+x4=x6;②2x+3y=5xy;③x6÷x3=x3;④(x3)2=x6.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.倒数是它本身的数是( )
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 0 |
 如图,点E在?ABCD的边CD的延长线上,AE∥BD,EF⊥BC且与BC的延长线相交于点F,求证:DF=$\frac{1}{2}$CE.
如图,点E在?ABCD的边CD的延长线上,AE∥BD,EF⊥BC且与BC的延长线相交于点F,求证:DF=$\frac{1}{2}$CE.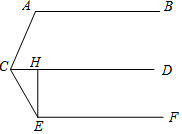 如图,已知AB∥CD∥EF,EH⊥CD,垂足为H,则∠A+∠CEH+∠ACE=270°.
如图,已知AB∥CD∥EF,EH⊥CD,垂足为H,则∠A+∠CEH+∠ACE=270°.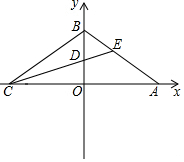 如图,直线y=-x+2与x轴交于点A,与y轴交于点B,点C在x轴上,且BC=BA,过C的直线与y轴交于点D,与线段AB交于点E.求使△OCD与△BDE面积相等时的直线CE的解析式.
如图,直线y=-x+2与x轴交于点A,与y轴交于点B,点C在x轴上,且BC=BA,过C的直线与y轴交于点D,与线段AB交于点E.求使△OCD与△BDE面积相等时的直线CE的解析式.