题目内容
9.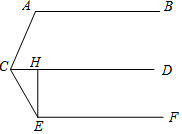 如图,已知AB∥CD∥EF,EH⊥CD,垂足为H,则∠A+∠CEH+∠ACE=270°.
如图,已知AB∥CD∥EF,EH⊥CD,垂足为H,则∠A+∠CEH+∠ACE=270°.
分析 根据两直线平行,同旁内角互补可得∠A+∠ACD=180°,根据垂直的定义求出∠CHE=90°,然后根据直角三角形两锐角互余求出∠DCE+∠CEH=90°,最后求解即可.
解答 解:∵AB∥CD,
∴∠A+∠ACD=180°,
∵EH⊥CD,
∴∠CHE=90°,
∴∠DCE+∠CEH=90°,
∴∠A+∠ACD+∠DCE+∠CEF=180°+90°=270°,
即∠A+∠CEH+∠ACE=270°.
故答案为:270°.
点评 本题考查了平行线的性质,垂线的定义,直角三角形两锐角互余,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
19. 如图所示的几何体的主视图为( )
如图所示的几何体的主视图为( )
 如图所示的几何体的主视图为( )
如图所示的几何体的主视图为( )| A. |  | B. |  | C. |  | D. |  |
20.以下图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.如图所示的四个“艺术字”中,轴对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列命题为真命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | n边形的外角和为(n-2)•180° | |
| D. | 三角形的一个外角等于它的两个内角的和 |
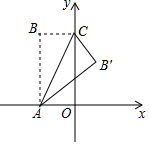 如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).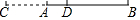 如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB,D为线段BC的中点.
如图,已知线段AB=a,延长BA至点C,使AC=$\frac{1}{2}$AB,D为线段BC的中点.