题目内容
5. 如图,点E在?ABCD的边CD的延长线上,AE∥BD,EF⊥BC且与BC的延长线相交于点F,求证:DF=$\frac{1}{2}$CE.
如图,点E在?ABCD的边CD的延长线上,AE∥BD,EF⊥BC且与BC的延长线相交于点F,求证:DF=$\frac{1}{2}$CE.
分析 由平行四边形的性质得出AB∥CD,AB=CD,证明四边形ABDE是平行四边形,得出AB=DE,因此CD=DE,再由直角三角形斜边上的中线性质即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CD=DE,
∵EF⊥BC,
∴DF=$\frac{1}{2}$CE.
点评 本题考查了平行四边形的性质与判定及直角三角形斜边上的中线性质;熟练掌握平行四边形的判定与性质,证出DE=CD是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.以下图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.-64的立方根是( )
| A. | -4 | B. | 8 | C. | -4和4 | D. | -8和8 |
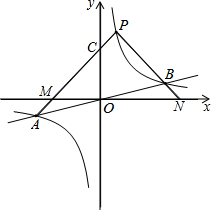 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B.点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A、B.点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.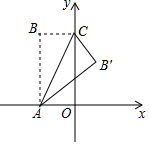 如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).