题目内容
4.解下列各题(1)先化简:(2x-$\frac{{x}^{2}+1}{x}$)÷$\frac{{x}^{2}-2x+1}{x}$,然后从0,1,-2中选择一个适当的数作为x的值代入求值.
(2)解方程:$\frac{3}{x+1}$=$\frac{x}{x-1}$-1.
分析 (1)先根据分式的基本性质化简原式,然后根据分式有意义的条件选一个适当的数代入即可求出x的值.
解答 解:(1)原式=(2x-$\frac{{x}^{2}+1}{x}$)÷$\frac{{(x-1)}^{2}}{x}$
=2x×$\frac{x}{{(x-1)}^{2}}$-$\frac{{x}^{2}+1}{x}$×$\frac{x}{{(x-1)}^{2}}$
=$\frac{x+1}{x-1}$
∵$\left\{\begin{array}{l}{x≠0}\\{x-1≠0}\end{array}\right.$
∴x≠0且x≠1
将x=-2代入$\frac{x+1}{x-1}$,
∴原式=-1
(2)3x-3=x2+x-x2+1
3x-3=x+1
3x-x=3+1
x=2
点评 本题考查学生的计算能力,解题的关键是熟练运用分式的基本性质,本题属于基础题型.

练习册系列答案
相关题目
19.下列命题为真命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | n边形的外角和为(n-2)•180° | |
| D. | 三角形的一个外角等于它的两个内角的和 |
13.下列各式中不正确的是( )
| A. | 22=(-2)2 | B. | -33=(-3)3 | C. | -22=(-2)2 | D. | -33=-|-33| |
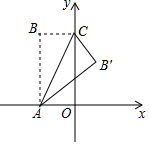 如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).
如图,矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=4,把△ABC沿着AC对折得到△AB'C,AB'交y轴于点D,则B'点的坐标为($\frac{6}{5}$,$\frac{12}{5}$).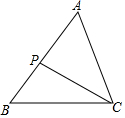 如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.
如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.