题目内容
10.已知扇形的圆心角为120°,面积为$\frac{25}{3π}$cm2.求扇形的弧长.分析 根据扇形面积公式S=$\frac{nπ{R}^{2}}{360}$和弧长公式l=$\frac{nπR}{180}$进行计算.
解答 解:∵扇形的圆心角为120°,面积为$\frac{25}{3π}$cm2,
∴$\frac{120π×{R}^{2}}{360}$=$\frac{25}{3π}$,
∴πR=5,
∴l=$\frac{120}{180}$πR=$\frac{2}{3}$×5=$\frac{10}{3}$.
点评 本题考查了弧长的计算和扇形面积的计算.解答该题需要牢记弧长公式和扇形的面积公式.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.在密码学中,把直接可以看到的内容称为明码,对明码进行某种处理后得到的内容称为密码.有一种密码,将英文26个字母a,b,c,…z依次对应1、2、3,…,26这26个自然数,如下表,当明码对应的序号x为奇数时,密码对应的序号y=$\frac{x+1}{2}$;当明码对应的序号x为偶数时,密码对应的序号y=$\frac{x}{2}+13$.
按上述规定,将明码“love”译成密码(密码是字母)是s、h、x、c.
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
2.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{0.5mn}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{27}$ | D. | $-\sqrt{125}$ |
20.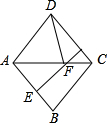 如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
 如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=100°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )| A. | 60° | B. | 50° | C. | 30° | D. | 20° |
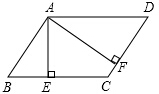 如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,AE⊥BC,AF⊥CD,若平行四边形ABCD的周长为48,AE=5,AF=10,则平行四边形ABCD的面积是80.