题目内容
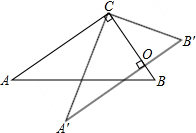 如图,在△ABC中,∠ACB=90°,将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,恰有BC与A′B′相交成直角,则图中与∠A互余的角有
如图,在△ABC中,∠ACB=90°,将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,恰有BC与A′B′相交成直角,则图中与∠A互余的角有考点:旋转的性质
专题:
分析:由在△ABC中,∠ACB=90°,可求得∠A+∠B=90°,将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,可得∠B=∠B′,∠A=∠A′,即可求得∠A+∠B′=90°,又由BC与A′B′相交成直角,可求得∠A+∠A′CB=90°.
解答:解:∵在△ABC中,∠ACB=90°,
∴∠A+∠B=90°,
∵将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,
∴∠B=∠B′,∠A=∠A′,
∴∠A+∠B′=90°,
∵BC与A′B′相交成直角,
∴∠A′+∠A′CB=90°,
∴∠A+∠A′CB=90°,
∴图中与∠A互余的角有3个.
故答案为:3.
∴∠A+∠B=90°,
∵将△ACB绕点C逆时针旋转使A转到A′点,B转到B′点,
∴∠B=∠B′,∠A=∠A′,
∴∠A+∠B′=90°,
∵BC与A′B′相交成直角,
∴∠A′+∠A′CB=90°,
∴∠A+∠A′CB=90°,
∴图中与∠A互余的角有3个.
故答案为:3.
点评:此题考查了旋转的性质以及直角三角形的性质.此题难度不大,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列方程是一元一次方程的是( )
| A、-5x+4=3y2 | ||||
| B、5(m2-1)=1-5m2 | ||||
C、2-
| ||||
| D、2(3p-2)=2p+2(2p-2) |
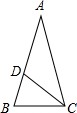 如图,在△ABC中,∠A=36°,∠B=72°,CD是∠ACD的平分线,则图中共有
如图,在△ABC中,∠A=36°,∠B=72°,CD是∠ACD的平分线,则图中共有 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BC=EF.
已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BC=EF.