题目内容
若x2-y2=5，（x+y）2=4，求x-y的值．
考点：平方差公式
专题：
分析：把（x+y）2=4两边开平方得到x+y=±2，然后根据平方差公式把x2-y2=5变形为（x+y）（x-y）=5，再代入计算整理即可求解．
解答：解：∵（x+y）2=4，
∴x+y=±2，
当x+y=-2时，x2-y2=（x+y）（x-y）=-2（x-y）=5，解得x-y=-2.5；
当x+y=2时，x2-y2=（x+y）（x-y）=2（x-y）=5，解得x-y=2.5．
故x-y的值为-2.5或2.5．
∴x+y=±2，
当x+y=-2时，x2-y2=（x+y）（x-y）=-2（x-y）=5，解得x-y=-2.5；
当x+y=2时，x2-y2=（x+y）（x-y）=2（x-y）=5，解得x-y=2.5．
故x-y的值为-2.5或2.5．
点评：本题考查了平方差公式，把已知条件（x+y）2=4两边开平方得到x+y=±2是解题的关键．
练习册系列答案
相关题目
把如图所示的图形沿虚线折叠，分别能折叠成什么几何体？观察制成的几何体，回答下列问题：
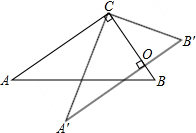如图，在△ABC中，∠ACB=90°，将△ACB绕点C逆时针旋转使A转到A′点，B转到B′点，恰有BC与A′B′相交成直角，则图中与∠A互余的角有
如图，直线AB，CD，EF相交于点O，已知∠AOC与∠COE互余，∠COE=25°，求∠BOD的度数．