题目内容
11.已知$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{2}{3}$,则$\frac{a+c+e}{b+d+f}$=$\frac{2}{3}$.分析 根据等比性质,可得答案.
解答 解:$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{2}{3}$,得$\frac{a}{b}$=$\frac{a+c+e}{b+d+f}$=$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查了比例的性质,利用等比性质:$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$⇒$\frac{a+c+e}{b+d+f}$=$\frac{a}{b}$是解题关键.

练习册系列答案
相关题目
1.如果a-b=0,那么下列结论中不一定成立的是( )
| A. | $\frac{a}{b}$=1 | B. | a2=b2 | C. | 2a=a+b | D. | a2=ab |
2.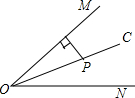 如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )
如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )
 如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )
如图:已知OC是∠MON的平分线,P是OC上一点,P到OM的距离为3cm,则P到ON的距离为( )| A. | 2cm | B. | 3cm | C. | 5cm | D. | 6cm |
19. 如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )
如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )
 如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )
如图,在平行四边形ABCD中,若∠B=60°,则∠D等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
6. 如图,DE∥BC,DE:BC=2:3,则△ADE与△ABC的面积之比是( )
如图,DE∥BC,DE:BC=2:3,则△ADE与△ABC的面积之比是( )
 如图,DE∥BC,DE:BC=2:3,则△ADE与△ABC的面积之比是( )
如图,DE∥BC,DE:BC=2:3,则△ADE与△ABC的面积之比是( )| A. | 2:3 | B. | 4:9 | C. | 3:2 | D. | 9:4 |
1.三角形两边的长分别是4和6,第三边的长是一元二次方程x2-16x+60=0的一个实数根,则该三角形的周长是( )
| A. | 16 | B. | 16或20 | C. | 20 | D. | 22 |
