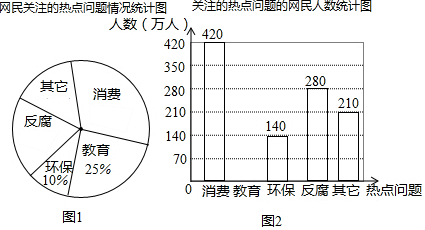
题目内容
15.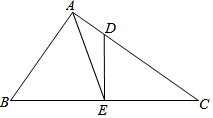 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
分析 由勾股定理求出BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=25,求出△ABC的面积=150,证明△CDE∽△CBA,得出$\frac{CE}{AC}=\frac{CD}{CB}$,求出CE=12,得出BE=BC-CE=13,再由三角形的面积关系即可得出答案.
解答 解:∵在Rt△ABC中,∠BAC=90°,AB=15,AC=20,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=25,△ABC的面积=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×15×20=150,
∵AD=5,
∴CD=AC-AD=15,
∵DE⊥BC,
∴∠DEC=∠BAC=90°,
又∵∠C=∠C,
∴△CDE∽△CBA,
∴$\frac{CE}{AC}=\frac{CD}{CB}$,即$\frac{CE}{20}=\frac{15}{25}$,
解得:CE=12,
∴BE=BC-CE=13,
∵△ABE的面积:△ABC的面积=BE:BC=13:25,
∴△ABE的面积=$\frac{13}{25}$×150=78;
故答案为:78.
点评 本题考查了相似三角形的判定与性质、勾股定理、三角形的面积;熟练掌握勾股定理,证明三角形相似是解决问题的关键

练习册系列答案
相关题目
11.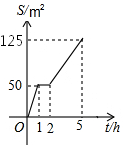 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
 园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息完后园林队每小时绿化面积为( )| A. | 75m2 | B. | 50m2 | C. | 31.25m2 | D. | 25m2 |
 如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图,则喜爱“体育”节目的人数是10人.
如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图,则喜爱“体育”节目的人数是10人.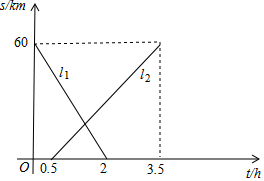 A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题: 如图,已知△ABC中,AB=4,AC=3.
如图,已知△ABC中,AB=4,AC=3.