��Ŀ����
10����ͼ����֪������y=-$\frac{1}{3}$x2+bx+1��y�ύ�ڵ�C����A��0��-$\frac{1}{2}$������B��1��0����ֱ��AB���������ཻ�ڵ�D����Eλ�ڵ�һ�����ڣ�����ֱ��AD�Ϸ���������D�����������ϣ�����EA��EB����1����ͼ1������C���������߶Գ���ĶԳƵ��ǵ�D��
���������ߵĽ���ʽ��
�������á�ABE�����ΪS����S��ȡֵ��Χ��
��2����ͼ2������D������Ϊ��-1��-1��������CD��CB������������x��Ľ���ΪF���ʣ��Ƿ���������ĵ�E��ʹ��tan��BDC��tan��EBF=1���������ڣ���������������ĵ�E�ĺ����ꣻ�������ڣ���˵�����ɣ�
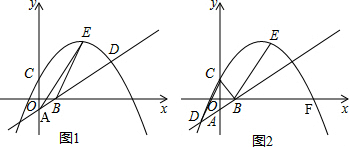
���� ��1���ٸ��������ߵĶԳ���x=$\frac{3}{2}$b��C��0��1���õ�D������Ϊ��3b��1�������ֱ��AB����ʽ������D�������ɵ�b��ֵ��
�������E����ABƽ�е�ֱ��Ϊy=$\frac{1}{2}$x+k������ֱ����������ֻ��һ��������ʱ������-$\frac{1}{3}$x2+x+1=$\frac{1}{2}$x+kֻ��һ��ʵ�������Ӷ����k��ֵ������֪��ֱ����x��Ľ��㣬���ֱ�ߵ�б�ʵó���ABE�ĸߣ����������ε������ʽ�ɵ����ֵ���Ӷ�֪S�ķ�Χ��
��2���ɵ�D��-1��-1����������߽���ʽ�����ݡ�DCB������ó�C��ֱ��AB�ľ��룬�Ӷ�֪sin��BDC=$\frac{\frac{3}{\sqrt{5}}}{\sqrt{5}}$=$\frac{3}{5}$��tan��BDC=$\frac{3}{4}$������tan��BDC��tan��EBF=1֪tan��EBF=$\frac{4}{3}$����E��x��-$\frac{1}{3}$x2+$\frac{5}{3}$x+1������$\frac{-\frac{1}{3}{x}^{2}+\frac{5}{3}x+1}{x-1}$=$\frac{4}{3}$����֮�ɵã�
��� �⣺��1���١������ߵĶԳ���Ϊx=$\frac{3}{2}$b������y��Ľ���C��0��1����
���D��������3b��1����
��A��0��$\frac{1}{2}$����B��1��0����
��ֱ��AB�Ľ���ʽΪy=$\frac{1}{2}$x-$\frac{1}{2}$��
����D��3b��1������ã�1=$\frac{3}{2}$b-$\frac{1}{2}$��
��ã�b=1��
�������ߵĽ���ʽΪy=-$\frac{1}{3}$x2+x+1��
�������E����ABƽ�е�ֱ��Ϊy=$\frac{1}{2}$x+k��
����ֱ����������ֻ��һ��������ʱ������
��-$\frac{1}{3}$x2+x+1=$\frac{1}{2}$x+k����-$\frac{1}{3}$x2-$\frac{1}{2}$x+k-1=0��
�ɡ�=0�ɵ�$\frac{1}{4}$-$\frac{4}{3}$��k-1��=0����ã�k=$\frac{19}{16}$��
��y=$\frac{1}{2}$x+$\frac{19}{16}$����x��Ľ���Ϊ��-$\frac{19}{8}$��0����
���ABE�ĸ�Ϊ��$\frac{19}{8}$+1��sin��ABO=$\frac{27}{8}$��$\frac{1}{\sqrt{5}}$��
��AB=$\frac{\sqrt{5}}{2}$��
��S�����ֵΪ$\frac{1}{2}$��$\frac{27}{8}$��$\frac{1}{\sqrt{5}}$��$\frac{\sqrt{5}}{2}$=$\frac{27}{32}$��
��0��S��$\frac{27}{32}$��
��2����D��-1��-1������y=-$\frac{1}{3}$x2+bx+1���ã�b=$\frac{5}{3}$��
��y=-$\frac{1}{3}$x2+$\frac{5}{3}$x+1��
�ߡ�DCB�����=$\frac{1}{2}$��$\frac{3}{2}$��2=$\frac{3}{2}$��
��C��ֱ��AB�ľ���Ϊ$\frac{\frac{3}{2}��2}{\sqrt{5}}$=$\frac{3}{\sqrt{5}}$��
��sin��BDC=$\frac{\frac{3}{\sqrt{5}}}{\sqrt{5}}$=$\frac{3}{5}$��
��tan��BDC=$\frac{3}{4}$��
��tan��BDC��tan��EBF=1��
��tan��EBF=$\frac{4}{3}$��
��E��x��-$\frac{1}{3}$x2+$\frac{5}{3}$x+1����
��$\frac{-\frac{1}{3}{x}^{2}+\frac{5}{3}x+1}{x-1}$=$\frac{4}{3}$��
��ã�x=$\frac{1+\sqrt{29}}{2}$��x=$\frac{1-\sqrt{29}}{2}$���ᣩ��
���E�ĺ�����Ϊ$\frac{1+\sqrt{29}}{2}$��
���� ������Ҫ������κ������ۺϣ��������մ���ϵ������������ʽ�������ε���������Ǻ�����Ӧ�ü��㵽ֱ�ߵľ��롢ƽ����ľ����ǽ���Ĺؼ���

| A�� | $\sqrt{2}$ | B�� | $\sqrt{3-��}$ | C�� | $\sqrt{{a}^{2}}$ | D�� | $\sqrt{\frac{1}{2}}$ |
 ��ͼ�������������������ȫ��ͬ��С��������ɵģ��뻭������������������ͬ��������״��
��ͼ�������������������ȫ��ͬ��С��������ɵģ��뻭������������������ͬ��������״��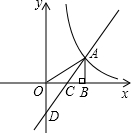 ��ͼ��ʾ����ֱ������ϵ�У���A�Ƿ���������y1=$\frac{k}{x}$��ͼ����һ�㣬AB��x�����������B�㣬C��OB���е㣻һ�κ���y2=ax+b��ͼ��A��C���㣬����y���ڵ�D��0��-2������S��AOD=4��
��ͼ��ʾ����ֱ������ϵ�У���A�Ƿ���������y1=$\frac{k}{x}$��ͼ����һ�㣬AB��x�����������B�㣬C��OB���е㣻һ�κ���y2=ax+b��ͼ��A��C���㣬����y���ڵ�D��0��-2������S��AOD=4��