题目内容
12.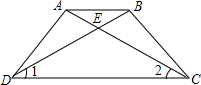 如图,已知AC,BD交于E,∠ADC=∠BCD,∠1=∠2,求证:AE=BF.
如图,已知AC,BD交于E,∠ADC=∠BCD,∠1=∠2,求证:AE=BF.
分析 根据∠ADC=∠BCD,∠1=∠2,求得∠ADB=∠BCA,根据等角对等边得到ED=EC,证明△AED≌△BEC,即可解答.
解答 解:∵∠ADC=∠BCD,∠1=∠2,
∴∠ADB=∠BCA,
∵∠1=∠2,
∴ED=EC,
在△AED和△BEC中,
$\left\{\begin{array}{l}{∠AED=∠BEC}\\{ED=EC}\\{∠ADE=∠BCE}\end{array}\right.$,
∴△AED≌△BEC,
∴AE=BF.
点评 本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,解决本题的关键是证明△AED≌△BEC.

练习册系列答案
相关题目
3.关于x的方程$\frac{m}{x-1}$=1的解为正数,则m的取值范围是( )
| A. | m>-1 | B. | m≠0 | C. | m>1且m≠0 | D. | m>-1且m≠0 |
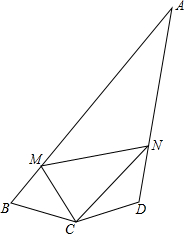 如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.
如图,四边形ABCD中,∠B+∠D=180°,∠BCD=150°,CB=CD,M,N为AB、AD上的两个动点,且∠MCN=75°.求证:MN=BM+DN.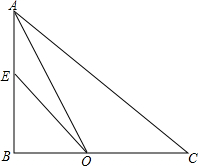 在△ABC中,∠ABC=90°,∠A的平分线AO交BC于O点,将线段OC绕点O逆时针旋转,使点C恰好落在边AB上E点处
在△ABC中,∠ABC=90°,∠A的平分线AO交BC于O点,将线段OC绕点O逆时针旋转,使点C恰好落在边AB上E点处  如图,由两个全等的梯形可以拼成一个菱形吗?符合什么条件的两个全等梯形可以凭此一个菱形?
如图,由两个全等的梯形可以拼成一个菱形吗?符合什么条件的两个全等梯形可以凭此一个菱形?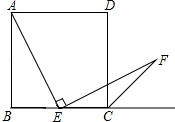 如图,点E是正方形ABCD中BC边上任意一点,以E为端点作EF=AE交∠BCD的外角平分线于F,求证:AE⊥EF.
如图,点E是正方形ABCD中BC边上任意一点,以E为端点作EF=AE交∠BCD的外角平分线于F,求证:AE⊥EF. 如图,在⊙O中,AB,CD为圆的两条弦,CD与OA,OB分别交于点E,F,且$\widehat{AC}=\widehat{BD}$,求证:OE=OF.
如图,在⊙O中,AB,CD为圆的两条弦,CD与OA,OB分别交于点E,F,且$\widehat{AC}=\widehat{BD}$,求证:OE=OF.