题目内容
20.若$\frac{2m-n}{n}$=$\frac{1}{3}$,则$\frac{m}{n}$=$\frac{2}{3}$;若x:y:z=2:4:7,且3x-y+2z=32,则x=4,y=8,z=14.分析 根据比例的性质:两内项积等于两外项积,再进行整理即可得出$\frac{m}{n}$的值;由x:y:z=2:4:7,可设x=2k,y=4k,z=7k代入3x-y+2z=32,可以求得k的值,从而可以求出x,y,z的值.
解答 解:∵$\frac{2m-n}{n}=\frac{1}{3}$,
∴3(2m-n)=n
∴6m=4n
∴$\frac{m}{n}=\frac{2}{3}$;
由x:y:z=2:4:7,
可设x=2k,y=4k,z=7k代入3x-y+2z=32得
6k-4k+14k=32
解得k=2
∴x=4,y=8,z=14.
故答案为:$\frac{1}{3}$;4,8,14.
点评 本题主要考查的是分式的性质:两内项积等于两外项积.解决此类问题的关键是根据题意发现各个量之间的关系并且得出相应的关系式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.某乡有四个村生产草莓,每千克售2.25元.填表:(用计算器计算)
| 村别 | 甲村 | 乙村 | 丙村 | 丁村 | 四村合计 |
| 数量(kg) | 12560 | 8974 | 9670 | 8796 | 40000 |
| 金额(元) | 28260 | 20191.5 | 21757.5 | 19791 | 90000 |
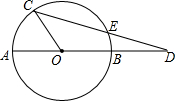 如图所示,AB是⊙0的直径,C是⊙0上一点,∠AOC=54°,CD交⊙0于点E,且DE=0A,求∠D的度数.
如图所示,AB是⊙0的直径,C是⊙0上一点,∠AOC=54°,CD交⊙0于点E,且DE=0A,求∠D的度数. 如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,求证:AO⊥BC.
如图,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O,求证:AO⊥BC.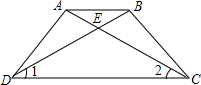 如图,已知AC,BD交于E,∠ADC=∠BCD,∠1=∠2,求证:AE=BF.
如图,已知AC,BD交于E,∠ADC=∠BCD,∠1=∠2,求证:AE=BF.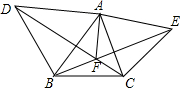 分别以△ABC的AB、AC为边向外作等边△ABD和等边△ACE,连结CD、BE交于F,求证:AF平分∠DFE.
分别以△ABC的AB、AC为边向外作等边△ABD和等边△ACE,连结CD、BE交于F,求证:AF平分∠DFE.