题目内容
6.如图1所示,一水库大坝横截面是梯形ABCD,坝顶宽6米,坝高23米,斜坡AB的坡度iAB=1:3,斜坡CD的坡度iCD=1:2.5.(1)求斜坡AB和坝底AD的长度;
(2)求斜坡CD的坡角α(精确到1°);
(3)若要把背水坡增加3米,同时背水坡AB的坡度iAB由原来的1:3变为1:5,如图2所示,请求出大坝的横截面的面积增加了多少平方米.
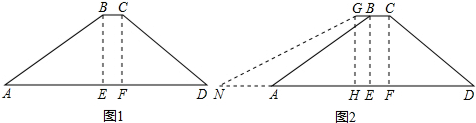
分析 (1)根据坡度和坡高求得AE和DF,然后根据勾股定理即可求得AB,进而即可求得AD;
(2)根据坡度即可求得;
(3)分别求得S梯形GNEB和S△BAE,然后根据S四边形GNAB=S梯形GNEB-S△BAE即可求得.
解答 解:(1)∵斜坡AB的坡度iAB=BE:AE=1:3,BE=23,
∴AE=69,
由勾股定理得,AB=23$\sqrt{10}$,
∵斜坡CD的坡度iCD═CF:DF=1:2.5,CF=23,
∴DF=57.5,
则AD=AE+EF+DF=134.5;
(2)tanα=1:2.5=0.4,
α≈22°;
(3)由题意得,GB=3m,GH=23m,
∵tan∠GNE=$\frac{GH}{NH}$=$\frac{1}{5}$,
∴NH=115m,
∵S梯形GNEB=$\frac{1}{2}$(GB+NE)•BE=$\frac{1}{2}$(3+115+3)×23=$\frac{1}{2}$×121×23,S△BAE=$\frac{1}{2}$BE•AE=$\frac{1}{2}$×23×69
∴S四边形GNAB=S梯形GNEB-S△BAE=$\frac{1}{2}$×121×23-$\frac{1}{2}$×23×69=$\frac{1}{2}$×23×52=498m2.
点评 此题考查了坡度坡角问题.此题难度适中,注意构造直角三角形,并借助于解直角三角形的知识求解是关键.

练习册系列答案
相关题目
14.下列函数中,y是x的一次函数的是y=3x;y=3+4x;2y=3x-4;2x+5y=0.6.
y=3x;y=3+4x;y=$\frac{1}{2}$;2y=3x-4;xy=3;2x+5y=0.6.
y=3x;y=3+4x;y=$\frac{1}{2}$;2y=3x-4;xy=3;2x+5y=0.6.
18.2的相反数和绝对值分别是( )
| A. | 2,2 | B. | -2,2 | C. | -2,-2 | D. | 2,-2 |
15.下列事件中,是随机事件的为( )
| A. | 水涨船高 | B. | 守株待兔 | C. | 水中捞月 | D. | 冬去春来 |
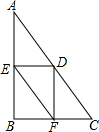 如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.
如图,△ABC中,∠B=90°,AB=8,BC=6,点D是AC上的任意一点,过点D作DE⊥AB于点E,DF⊥BC于点F,连接EF,则EF的最小值是4.8.