题目内容
15.-mx4+(m-3)x3-(2n-1)x2+hx不含x3和x2的项,写出这个多项式,求x=-1时多项式的值.分析 根据多项式不含x3和x2的项,则含x3和x2的项的系数为0,求出m,n的值,即可解答.
解答 解:∵-mx4+(m-3)x3-(2n-1)x2+nx不含x3和x2的项,
∴m-3=0,2n-1=0,
解得:m=3,n=$\frac{1}{2}$,
∴多项式为:-3x4+$\frac{1}{2}$x,
当x=-1时,原式=$-3×(-1)^{4}+\frac{1}{2}×(-1)$=-$\frac{7}{2}$.
点评 本题考查了多项式,多项式不含有的项的系数为零是解题关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
5.-3,0,-1,2四个数中,绝对值最大的数是( )
| A. | -3 | B. | 0 | C. | 2 | D. | -1 |
6.已知⊙O的半径为2,则⊙O的内接正三角形的面积为( )
| A. | $\frac{3}{2}\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
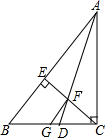 如图,在直角△ABC中,∠ACB=90°,∠BAC的平分线交BC于D,CE⊥AB于点E,交AD于点F,取BG=CD,连接FG,求证:FG∥AB.
如图,在直角△ABC中,∠ACB=90°,∠BAC的平分线交BC于D,CE⊥AB于点E,交AD于点F,取BG=CD,连接FG,求证:FG∥AB.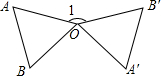 如图,将等边△OAB绕O点按逆时针方向旋转150°,得到△OA′B′(点A′,B′分别是点A,B的对应点),则∠1=150°.
如图,将等边△OAB绕O点按逆时针方向旋转150°,得到△OA′B′(点A′,B′分别是点A,B的对应点),则∠1=150°.