题目内容
4.若1<x<2,求代数式$\frac{x-2}{|x-2|}$-$\frac{1-x}{|x-1|}$+$\frac{|x|}{x}$的值.分析 由1<x<2,得出1-x<0,x-2<0,进一步根据绝对值的意义化简得出答案即可.
解答 解:∵1<x<2,
∴1-x<0,x-2<0,
∴代数式$\frac{x-2}{|x-2|}$-$\frac{1-x}{|x-1|}$+$\frac{|x|}{x}$=-1-(-1)+1=1.
点评 此题考查代数式求值,掌握绝对值的意义是解决问题的关键.

练习册系列答案
相关题目
19.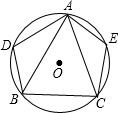 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )| A. | 220° | B. | 230° | C. | 240° | D. | 250°° |
 如图,在直角坐标系中,点A的坐标是(2,0),点B的坐标是(0,3),以AB为腰作等腰三角形,则另一顶点在坐标轴上的有4个.
如图,在直角坐标系中,点A的坐标是(2,0),点B的坐标是(0,3),以AB为腰作等腰三角形,则另一顶点在坐标轴上的有4个.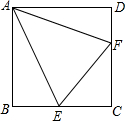 如图所示,在正方形ABCD中,E是CD上的任意一点,以AE为一边作∠EAF=45°,射线AF交BC于F点,连接EF,求证:EF=DE+BF.
如图所示,在正方形ABCD中,E是CD上的任意一点,以AE为一边作∠EAF=45°,射线AF交BC于F点,连接EF,求证:EF=DE+BF.
 如图,OP平分∠BOA,∠BOA=45°,PC∥OA,PD⊥OA.若PC=2$\sqrt{2}$,求PD的长度.
如图,OP平分∠BOA,∠BOA=45°,PC∥OA,PD⊥OA.若PC=2$\sqrt{2}$,求PD的长度.