题目内容
4．
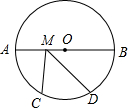如图，⊙O的半径是8，AB是⊙O的直径，M为AB上一动点，$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$，则CM+DM的最小值为16．
分析 作点C关于AB的对称点C′，连接C′D与AB相交于点M，根据轴对称确定最短路线问题，点M为CM+DM的最小值时的位置，根据垂径定理可得$\widehat{AC}$=$\widehat{AC′}$，然后求出C′D为直径，从而得解．
解答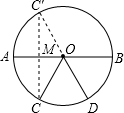 
解：如图，作点C关于AB的对称点C′，连接C′D与AB相交于点M，
此时，点M为CM+DM的最小值时的位置，
由垂径定理，$\widehat{AC}$=$\widehat{AC′}$，
∴$\widehat{BD}$=$\widehat{AC′}$，
∵$\widehat{AC}$=$\widehat{CD}$=$\widehat{BD}$，AB为直径，
∴C′D为直径，
∴CM+DM的最小值是16．
故答案是：16．
点评 本题考查了轴对称确定最短路线问题，垂径定理，熟记定理并作出图形，判断出CM+DM的最小值等于圆的直径的长度是解题的关键．
练习册系列答案
相关题目
14．已知x+y=2，xy=-1，则x2+y2的值为（ ）
| A． | 4 | B． | 2 | C． | -2 | D． | 6 |
一次函数y=-3x+b和y=kx+1的图象如图所示，其交点为P（3，4），则不等式（3+k）x≥b-1的解集是x≥3．
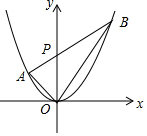若三角形的一边和该边上的高相等的三角形称为“和谐三角形”，如图，已知抛物线y=ax2经过A（-1，1），P是y轴正半轴上的动点，射线AP与抛物线交于另一点B，当△AOP是“和谐三角形”时，点B的坐标为（2，4）和（1，1）．
小明的爸爸承包了一个鱼塘，小明想知道鱼塘的长（即A，B间的距离）．他通过下面的方法测量A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测得MN的长为20m，由此他就知道了A，B间的距离．请你回答A，B间的距离是40m．