题目内容
10.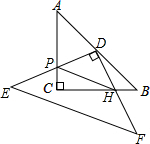 如图,在△ABC中,AC=BC,∠ACB=90°.现将一个三角板DEF的直角顶点D放在AB的中点处.两条直角边DE、DF分别与AC、BC相交于点P、H,连接PH.
如图,在△ABC中,AC=BC,∠ACB=90°.现将一个三角板DEF的直角顶点D放在AB的中点处.两条直角边DE、DF分别与AC、BC相交于点P、H,连接PH.(1)请判断△DPH的形状,并说明理由;
(2)求证:BH+AP=BC.
分析 (1)连接CD,求出∠PCD=∠B,∠PDC=∠HDB,DC=DB,证△PDC≌△HDB即可;
(2)由(1)知△PDC≌△HDB,则有PC=BH,从而可以证得结论.
解答 (1)△DPH为等腰直角三角形
证明:连接CD,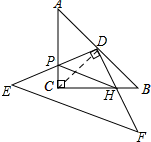
∵△ABC中,AB=BC,∠ABC=90°,D为AC中点,
∴BD=DC=$\frac{1}{2}$AB,∠ACD=∠BCD=∠A=∠B=45°,CD⊥AB,
∴∠BDC=90°=∠EDF,
∴∠PDC=∠HDB=90°-∠CDH,
在△PDC和△HDB中,
$\left\{\begin{array}{l}{∠PCD=∠B}\\{DC=DB}\\{∠PDC=∠HDB}\end{array}\right.$
△PDC≌△HDB(ASA),
∴PD=DH,
∴△DPH为等腰直角三角形.
(2)由(1)知△PDC≌△HDB,
∴PC=BH,
∴AC=BC=AP+PC=BH+AP,
∴BH+AP=BC.
点评 解决本题主要利用ASA求三角形全等,还运用了全等三角形的性质,等腰直角三角形的性质;解决此题的关键是掌握全等三角形的判定和性质.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
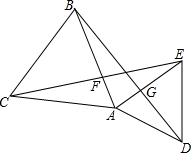 已知△ABC和△DAE是等边三角形,CE与AB交于点F,BD与AE交于点G,试问CE=BD吗?请说明你的结论.
已知△ABC和△DAE是等边三角形,CE与AB交于点F,BD与AE交于点G,试问CE=BD吗?请说明你的结论.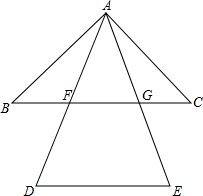 如图,已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE且∠DAB=∠EAC,则DE∥BC吗?为什么?
如图,已知△ABC和△ADE都是等腰三角形,AB=AC,AD=AE且∠DAB=∠EAC,则DE∥BC吗?为什么?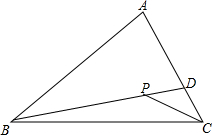 已知在三角形ABC中,存在一点P,连接PB、PC,延长BP交AC于点D,求证:AB+AC>PB+PC.
已知在三角形ABC中,存在一点P,连接PB、PC,延长BP交AC于点D,求证:AB+AC>PB+PC.
 某校为了了解八年级学生的身体发育情况,从全体八年级的学生中抽取了一些学生进行身高测量,所得数据如图,则该校的八年级学生的平均身高为162cm.
某校为了了解八年级学生的身体发育情况,从全体八年级的学生中抽取了一些学生进行身高测量,所得数据如图,则该校的八年级学生的平均身高为162cm.