题目内容
2.先化简再求值:$\frac{y}{x-y}+\frac{y^3}{{{x^3}-2{x^2}y+x{y^2}}}÷\frac{{xy+{y^2}}}{{y{\;}^2-{x^2}}}$,其中x,y是方程组$\left\{\begin{array}{l}2x+y=5\\ x-y=4\end{array}\right.$的解.分析 原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算得到最简结果,求出方程组的解得到x与y的值,代入计算即可求出值.
解答 解:原式=$\frac{y}{x-y}$+$\frac{{y}^{3}}{x(x-y)^{2}}$•$\frac{-(x+y)(x-y)}{y(x+y)}$=$\frac{y}{x-y}$+$\frac{-{y}^{2}}{x(x-y)}$=$\frac{y(x-y)}{x(x-y)}$=$\frac{y}{x}$,
方程组$\left\{\begin{array}{l}{2x+y=5①}\\{x-y=4②}\end{array}\right.$,
①+②得:3x=9,即x=3,
把x=3代入②得:y=-1,
则原式=$\frac{y}{x}$=-$\frac{1}{3}$.
点评 此题考查了分式的化简求值,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.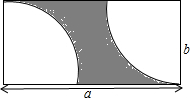 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )
 如图所示,阴影部分的面积是(其中a>2b)( )
如图所示,阴影部分的面积是(其中a>2b)( )| A. | ab-$\frac{π{a}^{2}}{4}$ | B. | ab-$\frac{π{b}^{2}}{2}$ | C. | ab-$\frac{π{a}^{2}}{2}$ | D. | ab-$\frac{π{b}^{2}}{4}$ |
18.甲厂有某种原料180吨,运出2x吨,乙厂有同样的原料120吨,运进x吨,现在甲厂原料比乙厂原料多30吨,根据题意列方程,则下列所列方程正确的是( )
| A. | (180-2x)-(120+x)=30 | B. | (180+2x)-(120-x)=30 | C. | (180-2x)-(120-x)=30 | D. | (180+2x)-(120+x)=30 |
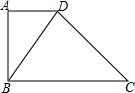 如图,已知四边形ABCD中,∠A=90°,AD∥BC.
如图,已知四边形ABCD中,∠A=90°,AD∥BC. 李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案:
李先生准备在永川某小区内购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是8000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李先生提供了以下两种优惠方案: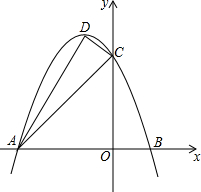 如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD.
如图抛物线y=ax2+bx+3与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,顶点为D,连接AC、CD、AD. 圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=40°.
圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=40°.