先将分式($\frac{x}{x-5}$-$\frac{x}{5-x}$)÷$\frac{2x}{{x}^{2}-25}$化简.然后再从-5≤x＜6的范围内选取一个使分式有意义的整数x代入求值．题目和参考答案——青夏教育精英家教网——

题目内容

2．先将分式（$\frac{x}{x-5}$-$\frac{x}{5-x}$）÷$\frac{2x}{{x}^{2}-25}$化简，然后再从-5≤x＜6的范围内选取一个使分式有意义的整数x代入求值．

分析先根据分式混合运算的法则把原式进行化简，再选出合适的x的值代入进行计算即可．

解答解：原式=（$\frac{x}{x-5}$+$\frac{x}{x-5}$）•$\frac{（x+5）（x-5）}{2x}$
=$\frac{2x}{x-5}$•$\frac{（x+5）（x-5）}{2x}$
=x+5．
当x=1时，原式=6．

点评本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案

初中毕业学业考试指南系列答案

绿色新课堂中考总复习系列答案

中考数学合成演练30天系列答案

汇测期末竞优系列答案

素质提优123系列答案

随堂练123系列答案

随堂新卷系列答案

堂堂清课堂8分钟小测系列答案

特级教师小学毕业升学系统总复习系列答案

提分计划单元期末系列答案

相关题目

12．已知点A（x₁，y₁）和点B（x₂，y₂）在反比例函数y=$\frac{k}{x}$（k＜0）的图象上，且x₁＜0＜x₂，判断y₁、y₂的大小关系：y₁＞y₂．（填“＞”、“=”、“＜”）

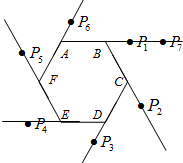将正六边形ABCDEF的各边按如图所示延长，从射线AB开始分别在各射线上标记点P₁、P₂、P₃、…，按此规律，点P₂₀₁₃在射线CD上．

如图，在下面的立方体中，它的主视图是（　　）

17．将一个五角星图片放大，当面积扩大为原来的9倍时，周长扩大为原来的（　　）

7．已知a+b≤5，-1≤a-b≤3，求3a-b的取值范围．

14．P（2，-3）关于x轴的对称的点在第（　　）象限．

11．把下列各数分别填入相应的集合内：
-7，3.5，-3.1415，π，0，$\frac{13}{17}$，0.03，-3$\frac{1}{2}$，10，-0.$\stackrel{..}{23}$，-$\frac{4}{2}$，0.1010010001…
自然数集合0，10，整数集合-7，0，10，-$\frac{4}{2}$，正分数集合3.5，$\frac{13}{17}$，0.03，非正数集合-7，-3.1415，0，-3$\frac{1}{2}$，-0.$\stackrel{..}{23}$，-$\frac{4}{2}$，有理数集合-7，3.5，-3.1415，0，$\frac{13}{17}$，0.03，-3$\frac{1}{2}$，10，-0.$\stackrel{..}{23}$，-$\frac{4}{2}$．

12．已知x-y=3，y-z=5，则x²+y²+z²-xy-yz-xz=49．