题目内容
4. 已知AB∥CD,EG平分∠BEF,FG平分∠EFD,请你说明EG⊥FG.
已知AB∥CD,EG平分∠BEF,FG平分∠EFD,请你说明EG⊥FG.
分析 根据两直线平行,同旁内角互补得到∠BEF+∠EFD=180°,再根据角平分线的定义可以求出∠1+∠2=90°,所以∠G=90°,即可得到EG与FG互相垂直.
解答 证明:∵AB∥CD,
∴∠BEF+∠EFD=180°,
∵EG平分∠BEF,FG平分∠DFE,
∴∠1=$\frac{1}{2}$∠BEF,∠2=$\frac{1}{2}$∠EFD,
∴∠1+∠2=$\frac{1}{2}$(∠BEF+∠EFD)=$\frac{1}{2}$×180°=90°,
在△EFG中,
∠G=180°-∠1-∠2=90°,
∴EG⊥FG.
点评 本题主要考查平行线的性质和角平分线的定义,熟练掌握性质和概念是解题的关键.

练习册系列答案
相关题目
16.下列各组数的大小比较中,正确的是( )
| A. | 1>2 | B. | -3>-2 | C. | 0>-1 | D. | $\sqrt{2}$>2 |
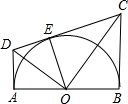 如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连结OD、OE、OC,对于下列结论:
如图,AB为半圆O的直径,AD、BC分别切⊙O于A,B两点,CD切⊙O于点E,AD与CD相交于D,BC与CD相交于C,连结OD、OE、OC,对于下列结论: 已知点A、B和直线l,求作:点P,使点P在直线l上,且PA=PB.
已知点A、B和直线l,求作:点P,使点P在直线l上,且PA=PB.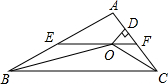 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+$\frac{1}{2}$∠A; ②EF=BE+CF;③设OD=m,AE+AF=n,则S△AEF=$\frac{1}{2}$mn; ④EF是△ABC的中位线.其中正确的结论是①②③.
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+$\frac{1}{2}$∠A; ②EF=BE+CF;③设OD=m,AE+AF=n,则S△AEF=$\frac{1}{2}$mn; ④EF是△ABC的中位线.其中正确的结论是①②③.