题目内容
6.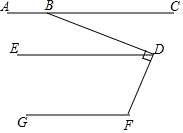 如图,已知AC∥ED,ED∥GF,∠BDF=90°.
如图,已知AC∥ED,ED∥GF,∠BDF=90°.(1)若∠ABD=150°,求∠GFD的度数;
(2)若∠ABD=θ,求∠GFD-∠CBD的度数.
分析 (1)根据平行线的性质可得∠ABD+∠BDE=180°,进而可得∠BDE=30°,然后再计算出∠EDF的度数,再根据平行线的性质可得∠EDF+∠F=180°,进而可得∠GFD的度数;
(2)与(1)类似,表示出∠F的度数,再表示出∠CBD的度数,再求差即可.
解答 解:(1)∵AC∥ED,
∴∠ABD+∠BDE=180°,
∵∠ABD=150°,
∴∠BDE=30°,
∵∠BDF=90°,
∴∠EDF=60°,
∵ED∥GF,
∴∠EDF+∠F=180°,
∴∠F=120°;
(2)∵AC∥ED,
∴∠ABD+∠BDE=180°,
∵∠ABD=θ,
∴∠BDE=θ,
∵∠BDF=90°,
∴∠EDF=(90-θ)°,
∵ED∥GF,
∴∠EDF+∠F=180°,
∴∠F=(90+θ)°,
∵∠ABD=θ,
∴∠CBD=(180-θ)°,
∴∠GFD-∠CBD=(90+θ)°-(180-θ)°=(2θ-90)°.
点评 此题主要考查了平行线的性质,关键是掌握两直线平行,同旁内角互补.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.等腰三角形的周长为21cm,如果它的一边长为5cm,那么其另两边长为( )
| A. | 5,8 | B. | 8,8 | C. | 5,11 | D. | 11,11 |
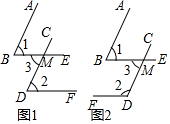 在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结论图形完成以下探究过程:
在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结论图形完成以下探究过程: 在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1). 如图,象棋盘上,若“将”位于点(1,-2),“车”位于点(-3,-2),则“马”位于点(4,1).
如图,象棋盘上,若“将”位于点(1,-2),“车”位于点(-3,-2),则“马”位于点(4,1).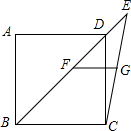 如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG.若AB=6,则FG的长度为( )
如图,已知在正方形ABCD中,连接BD并延长至点E,连接CE,F、G分别为BE,CE的中点,连接FG.若AB=6,则FG的长度为( ) 如图是由4个大小相同的正方体组合而成的几何体,其左视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其左视图是( )



 若实数a满足|a-$\frac{1}{2}$|=$\frac{3}{2}$,则a对应于图中数轴上的点可以是A、B、C三点中的点B.
若实数a满足|a-$\frac{1}{2}$|=$\frac{3}{2}$,则a对应于图中数轴上的点可以是A、B、C三点中的点B.