题目内容
4.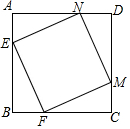 如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8.
如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8.
分析 应该是正方形.可通过证明三角形AEN,DNM,MCF,FBE全等,先得出四边形ENMF是菱形,再证明四边形EFMN中一个内角为90°,从而得出四边形EFMN是正方形的结论.
解答 解:∵AE=BF=CM=DN,
∴AN=DM=CF=BE.
∵∠A=∠B=∠C=∠D=90°,
∴△AEN≌△DMN≌△CFM≌△BEF.
∴EF=EN=NM=MF,∠ENA=∠DMN.
∴四边形EFMN是菱形.
∵∠ENA=∠DMN,∠DMN+∠DNM=90°,
∴∠ENA+∠DNM=90°.
∴∠ENM=90°.
∴四边形EFMN是正方形,
∴EN最小时,正方形EFMN的面积最小,设AE=DN=x,
则EN=$\sqrt{{x}^{2}+(4-x)^{2}}$=$\sqrt{2(x-2)^{2}+8}$,
∴x=2时,EN的值最小,最小值=$\sqrt{8}$,
∴正方形EFMN的面积=($\sqrt{8}$)2=8.
点评 本题主要考查了正方形的性质和判定,全等三角形的判定和性质,二次函数的性质等知识,解题的关键是正确寻找全等三角形解决问题,学会构建二次函数解决最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列调查中,调查方式选择错误的是( )
| A. | 为了解全市中学生的课外阅读情况,选择全面调查 | |
| B. | 旅客上飞机前的安检,选择全面调查 | |
| C. | 为了了解《人民的名义》的收视率,选择抽样调查 | |
| D. | 为保证“神舟十一号”载人飞船的成功发射,对其零部件的检查,选择全面调查 |
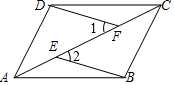 如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形. 在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).