题目内容
若x2+2（m-3）x+25是一个完全平方式，则m的值为（ ）
| A、6或-3 | B、8或-2 |
| C、8 | D、-5或3 |
考点：完全平方式
专题：
分析：先根据两平方项确定出这两个数，再根据完全平方公式的乘积二倍项即可确定m的值．
解答：解：∵x2+2（m-3）x+25=x2+2（m-3）x+52，
∴2（m-3）x=2×x×5或2（m-3）x=-2×x×5，
解得m=8或m=-2．
故选B．
∴2（m-3）x=2×x×5或2（m-3）x=-2×x×5，
解得m=8或m=-2．
故选B．
点评：本题主要考查了完全平方式，根据平方项确定出这两个数是解题的关键，也是难点，熟记完全平方公式对解题非常重要．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
如图，有两条抛物线y=ax2（a＞0），y=mx2+nx（m＜0），抛物线y=mx2+nx的顶点在y=ax2上，且与x轴交于（0，0），（4，0）两点，则不等式（a-m）x2-nx＜0的解集是
已知△ABC中，AC=6，D是AC的中点，BD=要使
、
、（2x-4）0三个式子都有意义，则x的取值范围应为（ ）
| x+1 |
| 1 | ||
|
A、x＞
| ||
| B、x≥-1且x≠2 | ||
C、x＞
| ||
D、
|
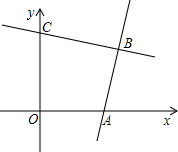已知：如图，直线y1=mx-3m与x轴交于点A，直线y2=kx+b与y轴交于点C，两直线交于点B．