题目内容
(本题满分8分)
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.
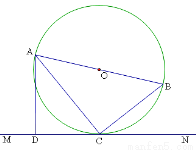
(1)猜想直线MN与⊙O的位置关系,并说明理由,
(2)若CD=6,cos∠ACD=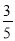 ,求⊙O的半径.
,求⊙O的半径.
(1)MN与⊙O相切,理由见解析;
(2)⊙O的半径为 .
.
【解析】
试题分析:(1)连接OC,由OA=OC,可得∠BAC=∠OCA,再由∠BAC=∠DAC,得∠OCA=∠DAC,从而AD∥OC, 由AD⊥MN,可得OC⊥MN,即MN与⊙O相切;
(2)由CD=6,cos∠ACD= ,可得AC=10,又由∠ACB=∠ADC,∠BAC=∠DAC,可得△ABC∽△ACD,利用相似比即可得AB的长,从而得半径长.
,可得AC=10,又由∠ACB=∠ADC,∠BAC=∠DAC,可得△ABC∽△ACD,利用相似比即可得AB的长,从而得半径长.
试题解析:(1)MN与⊙O相切,
理由:连接OC, ∵OA=OC,∴∠BAC=∠OCA,∵∠BAC=∠DAC,∴∠OCA=∠DAC,∴AD∥OC, ∵AD⊥MN, ∴OC⊥MN,∵OC为⊙O的半径, ∴MN与⊙O相切;

(2)∵AD⊥MN, ∴∠ADC=90°,∴AC= =6÷
=6÷ =10,∴AD=
=10,∴AD= =8,∵AB是⊙O的直径,∴∠ACB=90°, ∴∠ACB=∠ADC, ∵∠BAC=∠DAC, ∴△ABC∽△ACD, ∴
=8,∵AB是⊙O的直径,∴∠ACB=90°, ∴∠ACB=∠ADC, ∵∠BAC=∠DAC, ∴△ABC∽△ACD, ∴ ,
,
∴AB= =
= =
= ,∴⊙O的半径为
,∴⊙O的半径为 .
.
考点:1、切线的判定与性质;2、三角函数的应用;3、相似三角形的判定与性质.

练习册系列答案
相关题目
 向下平移6个单位,所得到的抛物线的顶点坐标为 .
向下平移6个单位,所得到的抛物线的顶点坐标为 .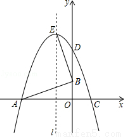


 ,∠B=
,∠B= ,则∠BAC= .
,则∠BAC= .
 小时;B、1小时<上网时间
小时;B、1小时<上网时间 小时;C、4小时<上网时间
小时;C、4小时<上网时间 小时;D、上网时间>7小时.统计
小时;D、上网时间>7小时.统计

 )米 C.12米 D.18米
)米 C.12米 D.18米