题目内容
(本题满分12分)
已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.

(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由.
(1)BE=2;
(2)存在满足条件的t,
【解析】
试题分析:(1)由于四边形BEFG为正方形,所以得GF∥BE,从而得△AGF∽△ABC,由相似比即可得正方形的边长,即BE长;
由已知条件可得△MEC∽△ABC,从而得ME的长,利用勾股定理分别求得△B′DM在三边长,然后分情况讨论即可.
试题解析:(1)如图①,设正方形BEFG的边长为x,则BE=FG=BG=x,∵AB=3,BC=6,∴AG=AB﹣BG=3﹣x,
∵GF∥BE,∴△AGF∽△ABC,∴ ,即
,即 ,解得:x=2,即BE=2;
,解得:x=2,即BE=2;

(2)存在满足条件的t,当t为 或﹣3+
或﹣3+ 时,△B′DM是直角三角形;
时,△B′DM是直角三角形;
理由:如图②,过点D作DH⊥BC于H,则BH=AD=2,DH=AB=3,由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t,∵EF∥AB,∴△MEC∽△ABC,∴ ,即
,即 ,∴ME=2﹣
,∴ME=2﹣ t,
t,
在Rt△B′ME中,B′M2=ME2+B′E2=22+(2﹣ t)2=
t)2= t2﹣2t+8,
t2﹣2t+8,
在Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13,
过点M作MN⊥DH于N,
则MN=HE=t,NH=ME=2﹣ t,
t,
∴DN=DH﹣NH=3﹣(2﹣ t)=
t)= t+1,
t+1,
在Rt△DMN中,DM2=DN2+MN2= t2+t+1,
t2+t+1,
(Ⅰ)若∠DB′M=90°,则DM2=B′M2+B′D2,
即 t2+t+1=(
t2+t+1=( t2﹣2t+8)+(t2﹣4t+13),
t2﹣2t+8)+(t2﹣4t+13),
解得:t= ,
,
(Ⅱ)若∠B′MD=90°,则B′D2=B′M2+DM2,
即t2﹣4t+13=( t2﹣2t+8)+(
t2﹣2t+8)+( t2+t+1),
t2+t+1),
解得:t1=﹣3+ ,t2=﹣3﹣
,t2=﹣3﹣ (舍去),
(舍去),
∴t=﹣3+ ;
;
(Ⅲ)若∠B′DM=90°,则B′M2=B′D2+DM2,
即: t2﹣2t+8=(t2﹣4t+13)+(
t2﹣2t+8=(t2﹣4t+13)+( t2+t+1),
t2+t+1),
此方程无解,
综上所述,当t为 或﹣3+
或﹣3+ 时,△B′DM是直角三角形;
时,△B′DM是直角三角形;
考点:1、正方形的性质;2、相似三角形的判定与性质;3、勾股定理;4、分类思想.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
A.3<x<3.23 B. 3.23<x<3.24 C. 3.24<x<3.25 D. 3.25<x<3.26
 -
- =2.
=2.
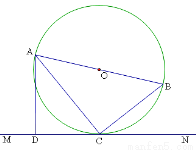
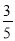 ,求⊙O的半径.
,求⊙O的半径.
 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
 )
)