题目内容
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )

A.2.5 B.1.6 C.1.5 D.1
B
【解析】
试题分析:连接OE、OD,∵⊙O与AC切于点D,与BC切于点E,∴∠OEC=∠ODC=90°,又∵∠C=90°,OD=OE,∴四边形OECD是正方形,∴OD//BC,CD=OD,∴ ,∵AD=AC-CD,AC=4,BC=6,∴
,∵AD=AC-CD,AC=4,BC=6,∴ ,∴OD=2.4,∴AD=4-2.4=1.6;
,∴OD=2.4,∴AD=4-2.4=1.6;
故选B.

考点:1、切线的性质;2、平行线分线段成比例定理.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
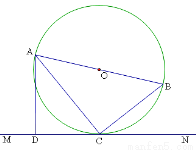
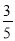 ,求⊙O的半径.
,求⊙O的半径.
 ,则EC的长是 ( )
,则EC的长是 ( )
 ,AB=10米,AE=15米.
,AB=10米,AE=15米.
 )
)