题目内容
7. 如图,在△ABC中,AB=AC,∠CAE是△ABC的一个外角.
如图,在△ABC中,AB=AC,∠CAE是△ABC的一个外角.(1)用尺规作图方法,按要求作图:
①作△ABC的高AD;
②作∠CAE的平分线AM;(要求:保留作图痕迹,不写作法和证明)
(2)判断(1)中的AM与BC的位置关系,并证明你的结论.
分析 (1)根据过直线外一点做已知直线垂线的方法作高AD;根据角平分线的作法作∠CAE的平分线AM;
(2)根据等腰三角形的性质可得∠CAD=$\frac{1}{2}$∠BAC,根据角平分线的性质可得∠CAM=$\frac{1}{2}$∠CAE,然后可得∠MAD的度数,再根据同一平面内,垂直于同一条直线的两直线平行可得结论.
解答 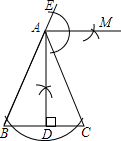 解:(1)如图:
解:(1)如图:
①AD为所作的△ABC的高;
②射线AM为所作的∠CAE的平分线.
(2)AM∥BC.
证明如下:
∵AB=AC,AD⊥BC,
∴∠CAD=$\frac{1}{2}$∠BAC.
∵AM是∠CAE的平分线,
∴∠CAM=$\frac{1}{2}$∠CAE,
∴∠CAD+∠CAM=$\frac{1}{2}$∠EAB=90°,
∴AD⊥AM,
∴AM∥BC.
点评 此题主要考查了复杂作图,以及平行线的判定,关键是掌握角平分线和过直线外一点做已知直线垂线的作图方法.

练习册系列答案
相关题目
18.如果单项式-ax-1b3与$\frac{1}{2}$bya2是同类项,那么x、y的值分别为( )
| A. | x=2,y=3 | B. | x=2,y=2 | C. | x=3,y=2 | D. | x=3,y=3 |
2. 如图,点A、F、C、D在同一直线上,AF=DC,BC∥EF,要判定△ABC≌△DEF,还需要添加一个条件,下列所添加的条件中错误的是( )
如图,点A、F、C、D在同一直线上,AF=DC,BC∥EF,要判定△ABC≌△DEF,还需要添加一个条件,下列所添加的条件中错误的是( )
 如图,点A、F、C、D在同一直线上,AF=DC,BC∥EF,要判定△ABC≌△DEF,还需要添加一个条件,下列所添加的条件中错误的是( )
如图,点A、F、C、D在同一直线上,AF=DC,BC∥EF,要判定△ABC≌△DEF,还需要添加一个条件,下列所添加的条件中错误的是( )| A. | BC=EF | B. | AB=DE | C. | AB∥ED | D. | ∠B=∠E |
19.下列命题,是假命题的是( )
| A. | 若直线y=kx-2经过第一、三、四象限,则k>0 | |
| B. | 三角形三边垂直平分线的交点到三个顶点的距离相等 | |
| C. | 等腰三角形的角平分线、中线和高互相重合 | |
| D. | 如果∠A和∠B是对顶角,那么∠A=∠B |
 如图,在Rt△ABC中,∠C=90°,线段AB的垂直平分线交AB于点D,交BC于点E,若AC=4,CE=3,求BE的长.
如图,在Rt△ABC中,∠C=90°,线段AB的垂直平分线交AB于点D,交BC于点E,若AC=4,CE=3,求BE的长. 如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2).
如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2). 如图,在半径为a的大圆中画四个直径为a的小圆,则图中阴影部分的面积为(πa2-2a2)(用含a的代数式表示,结果保留π).
如图,在半径为a的大圆中画四个直径为a的小圆,则图中阴影部分的面积为(πa2-2a2)(用含a的代数式表示,结果保留π).