题目内容
17．
如图，在半径为a的大圆中画四个直径为a的小圆，则图中阴影部分的面积为（πa2-2a2）（用含a的代数式表示，结果保留π）．
分析 根据圆的中心对称性，通过移动不难发现：阴影部分的面积=大圆的面积-边长为$\sqrt{2}$a的正方形面积．
解答 解；观察图形，把里面的阴影图形，分成8个弓形，移动到如右图位置，
∴S阴=
大圆的面积-边长为$\sqrt{2}$a的正方形面积=πa2-（$\sqrt{2}$a）2=πa2-2a2．
故答案为（πa2-2a2）．
点评 本题考查正方形、圆面积公式，将不规则图形面积转化为规则图形的面积是解决这类题目的关键．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
如图，在△ABC中，AB=AC，∠CAE是△ABC的一个外角．
8．
如图，在△ABC中，D、E分别是AB、AC上的点，且DE∥BC，若S△ADE：S△ABC=4：9，则AD：BD=（ ）
如图，在△ABC中，D、E分别是AB、AC上的点，且DE∥BC，若S△ADE：S△ABC=4：9，则AD：BD=（ ）| A． | 2：1 | B． | 1：2 | C． | 2：3 | D． | 4：9 |
5．
如图，在△ABC中，∠ABC=60°，BC=6，CD是△ABC的一条高线．若E，F分别是CD和BC上的动点，则BE+EF的最小值是（ ）
如图，在△ABC中，∠ABC=60°，BC=6，CD是△ABC的一条高线．若E，F分别是CD和BC上的动点，则BE+EF的最小值是（ ）| A． | 6 | B． | 3$\sqrt{2}$ | C． | 3$\sqrt{3}$ | D． | 3 |
一个几何体的三个视图如图所示（单位：cm）．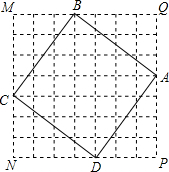
如图，正方形MNPQ网格中，每个小方格的边长都相等，正方形ABCD的顶点在正方形MNPQ的4条边的小方格顶点上．