题目内容
15. 菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.
菱形ABCD的边AB为5,对角线AC为8,则菱形ABCD的面积为24.
分析 连接BD,交AC于O,根据菱形的两条对角线互相垂直且平分可得AO=CO=$\frac{1}{2}$AC=4,BO=DO,CA⊥BD,然后利用勾股定理计算出BO的长,进而可得BD长,再利用菱形的面积公式进行计算即可.
解答 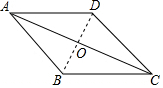 解:连接BD,交AC于O,
解:连接BD,交AC于O,
∵四边形ABCD是菱形,
∴AO=CO=$\frac{1}{2}$AC=4,BO=DO,CA⊥BD,
∵AB=5,
∴BO=$\sqrt{A{B}^{2}-A{O}^{2}}$=3,
∴BD=6,
∴菱形ABCD的面积为:$\frac{1}{2}×$6×8=24,
故答案为:24.
点评 此题主要考查了菱形的性质,关键是掌握菱形的两条对角线互相垂直且平分.

练习册系列答案
相关题目
4.某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在50≤x≤120时,具有一次函数的关系,如表所示.
(1)求y关于x的函数解析式;
(2)如果修建70天,那么平均每天的修建费是多少?
| x | 50 | 80 | 100 | 120 |
| y | 40 | 34 | 30 | 26 |
(2)如果修建70天,那么平均每天的修建费是多少?
11.下列各式中正确的是( )
| A. | 2-3=8 | B. | -2-3=$\frac{1}{8}$ | C. | -2-3=-$\frac{1}{8}$ | D. | (2017-π)0=0 |
20.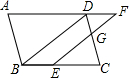 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
 如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )
如图,平行四边形ABCD,点E在边BC上,点F在AD边的延长线上,且EF∥BD,EF,CD交于点G,$\frac{DF}{AD}$=$\frac{2}{5}$,S四边形BDGE=a,则S平行四边形ABCD的值为( )| A. | $\frac{25a}{8}$ | B. | $\frac{25a}{9}$ | C. | $\frac{25a}{16}$ | D. | $\frac{16a}{9}$ |
2.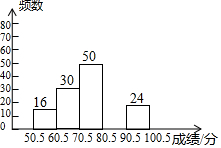 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
请根据所给信息,解答下列问题:
(1)表中m=80,n=0.12;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,分别求出被抽取的学生中优秀的学生频数和频率.
 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5-60.5 | 16 | 0.08 |
| 二 | 60.5-70.5 | 30 | 0.15 |
| 三 | 70.5-80.5 | 50 | 0.25 |
| 四 | 80.5-90.5 | m | 0.40 |
| 五 | 90.5-100.5 | 24 | n |
(1)表中m=80,n=0.12;
(2)补全频数分布直方图;
(3)若成绩超过80分为优秀,分别求出被抽取的学生中优秀的学生频数和频率.
3.已知正比例函数y=(k-2)x的图象经过第一、三象限,则k的值可能是( )
| A. | -2 | B. | 2 | C. | 3 | D. | 0 |
 =____________________。
=____________________。