Question

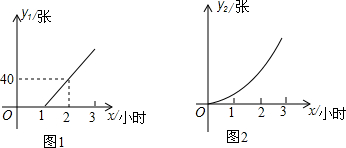
11．某动车站在原有的普通售票窗口外新增了无人售票窗口，普通售票窗口从上午8点开放，而无人售票窗口从上午7点开放，某日从上午7点到10点，每个普通售票窗口售出的车票数y₁（张）与售票时间x（小时）的变化趋势如图1，每个无人售票窗口售出的车票数y₂（张）与售票时间x（小时）的变化趋势是以原点为顶点的抛物线的一部分，如图2，若该日截至上午9点，每个普通售票窗口与每个无人售票窗口售出的车票数恰好相同．
（1）求图2中所确定抛物线的解析式；
（2）若该日共开放5个无人售票窗口，截至上午10点，两种窗口共售出的车票数不少于900张，则至少需要开放多少个普通售票窗口？

Answer 1

分析 （1）设${y}_{2}=a{x}^{2}$，当x=2时，y₁=y₂=40，利用待定系数法即可解答；
（2）设y₁=kx+b（1≤x≤3），把（1，0），（2，40）分别代入y₁=kx+b，求得y₂=40x-40，当x=3时，y₁=80，y₂=90，设需要开放m个普通售票窗口，所以80m+90×5≥900，解得m≥5$\frac{5}{8}$，因为m取整数，所以m≥6，即可解答．

解答 解：（1）设${y}_{2}=a{x}^{2}$，
当x=2时，y₁=y₂=40，
把（2，40）代入${y}_{2}=a{x}^{2}$，
4a=40，
解得：a=10，
∴${y}_{2}=10{x}^{2}$．
（2）设y₁=kx+b（1≤x≤3），
把（1，0），（2，40）分别代入y₁=kx+b得：
$\left\{\begin{array}{l}{k+b=0}\\{2k+b=40}\end{array}\right.$
解得：$\left\{\begin{array}{l}{k=40}\\{b=-40}\end{array}\right.$，
∴y₁=40x-40，
当x=3时，y₁=80，y₂=90，
设需要开放m个普通售票窗口，
∴80m+90×5≥900，
∴m≥5$\frac{5}{8}$，
∴m取整数，
∴m≥6．
答：至少需要开放6个普通售票窗口．

点评 本题考查了一次函数的应用，解决本题的关键是利用待定系数法求函数解析式．