题目内容
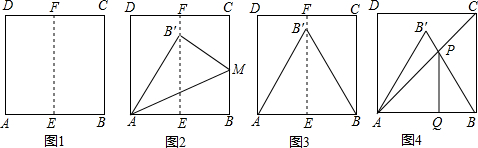
1.(一)实践与操作第一步:取一张正方形纸片ABCD,按图1对折,得折痕EF,摊开展平;
第二步:将B点折到EF上B′,如图2.
(二)解决问题
(1)如图3,连接BB′,试判定△ABB′的形状,并证明你的结论;
(2)如图4,连接AC,交BB′于P,作PQ⊥AB于Q,若AB=2,求PQ.
分析 (1)首先根据折叠的性质,推得AB'=AB;然后根据EF是AB的垂直平分线,B'是EF上的一点,推得AB'=BB',据此可得AB'=BB'=AB,所以△ABB'是等边三角形,据此判断即可.
(2)首先根据四边形ABCD是正方形,AC是正方形ABCD的对角线,PQ⊥AB,推得△APQ是等腰直角三角形;然后根据△ABB'是等边三角形,可得∠ABP=60°;最后设BQ=x,则AQ=PQ=$\sqrt{3}x$,根据AQ+BQ=AB,求出x的值是多少,进而求出PQ的值是多少即可.
解答 (1)证明:由折叠的性质,可得AB'、AB关于AM对称,
∴AB'=AB,
∵EF是AB的垂直平分线,B'是EF上的一点,
∴AB'=BB',
∴AB'=BB'=AB,
∴△ABB'是等边三角形.
(2)解:∵四边形ABCD是正方形,AC是正方形ABCD的对角线,PQ⊥AB,
∴△APQ是等腰直角三角形,
∵△ABB'是等边三角形,
∴∠ABP=60°,
设BQ=x,
则AQ=PQ=$\sqrt{3}x$,
∵AQ+BQ=AB,
∴$\sqrt{3}x+x=2$,
∴x=$\frac{2}{\sqrt{3}+1}$=$\sqrt{3}-1$,
∴PQ=$\sqrt{3}(\sqrt{3}-1)=3-\sqrt{3}$.
点评 (1)此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了等边三角形的判定和性质的应用,要熟练掌握.

练习册系列答案
相关题目
5.一次函数y=2x-4的图象与两坐标轴交点的距离是( )
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
6.正比例函数y=-3x的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
3.实验中学为了了解该校学生课外阅读情况,随机抽查了50名学生,统计他们平均每周课外阅读时间t(h).枨据时间t的长短分为A,B,C,D四类.下面是根据所抽杳的人数绘制了不完整的统计表.其中a、b、c和d是满足a<b<c<d的正整数,请解答下面的问题:
50名学生平均每天课外阅读时间统计表
(1)写出表格中a+b+c+d的值.并求表格中的a、b、c、d的值;
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
50名学生平均每天课外阅读时间统计表
| 类别 | A | B | C | D |
| 时间t(h) | t<1 | 1≤t<2 | 2≤t<3 | t≥3 |
| 人数 | 5a | 5b | 5c | 5d |
(2)如果每分钟阅读200个字,每天坚持课外阅读时间为0.5h,一年(365天)能阅读多少本(10万字/本)书籍?
13.某工艺品商店购进一款进价为10元/件的工艺品进行试销,经过一段时间的销售得到如下数据:
(1)根据表格中的对应关系,猜想y与x的函数关系,并求出该函数关系式;
(1)当销售单价定为多少时,商店试销该工艺品每天获得的利润最大?(利润=销售总价-成本总价)
(2)若物价部门规定,这种工艺品的销售单价不能超过38元,那么工艺品商店应该将工艺品的销售单价定为多少时,使每天销售该工艺品获得的利润最大?最大利润是多少?
| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 50 | 40 | 30 | 20 | 10 | … |
(1)当销售单价定为多少时,商店试销该工艺品每天获得的利润最大?(利润=销售总价-成本总价)
(2)若物价部门规定,这种工艺品的销售单价不能超过38元,那么工艺品商店应该将工艺品的销售单价定为多少时,使每天销售该工艺品获得的利润最大?最大利润是多少?
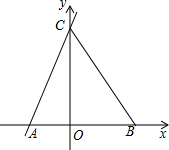 如图,已知点(-2,0),B(3,0),C(0,6),连接BC.
如图,已知点(-2,0),B(3,0),C(0,6),连接BC.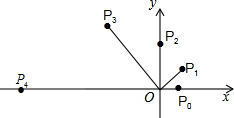 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…,则
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…,则 如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为6$\sqrt{2}$.
如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则线段AP+BP+PD的最小值为6$\sqrt{2}$.