题目内容
6.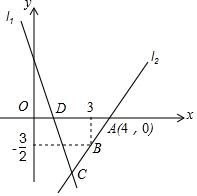 如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C,在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标是(6,3).
如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C,在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请写出点P的坐标是(6,3).
分析 根据点A、B的坐标利用待定系数法求出直线l2的解析表达式,联立直线l1、l2解析表达式成方程组,解之即可得出点C的坐标,再根据△ADP与△ADC的面积相等且底边AD相等,即可得出点P的纵坐标,利用一次函数图象上点的坐标特征即可求出点P的坐标.
解答 解:设直线l2的解析表达式为y=kx+b(k≠0),
将A(4,0)、B(3,-$\frac{3}{2}$)代入y=kx+b中,
$\left\{\begin{array}{l}{4k+b=0}\\{3k+b=-\frac{3}{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-6}\end{array}\right.$,
∴直线l2的解析表达式为y=$\frac{3}{2}$x-6.
联立直线l1、l2解析表达式成方程组,
$\left\{\begin{array}{l}{y=-3x+3}\\{y=\frac{3}{2}x-6}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$,
∴点C的坐标为(2,-3).
∵△ADP与△ADC的面积相等,且底边AD相等,
∴点P的纵坐标为3.
当y=$\frac{3}{2}$x-6=3时,x=6,
∴点P的坐标为(6,3).
故答案为:(6,3).
点评 本题考查了两条直线相交或平行问题、解一元一次方程组、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,根据点A、B的坐标利用待定系数法求出直线l2的解析表达式是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
11.为了解石柱中学初2017届男生的身高,从中抽取了6名男生,测得身高(单位:cm)为:160,175,170,158,164,157,则这组数据的中位数和极差分别是( )
| A. | 161,18 | B. | 162,17 | C. | 162,18 | D. | 161,17 |
18.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-1,2),则这个函数的图象一点经过( )
| A. | (-2,1) | B. | ($-\frac{1}{2}$,2) | C. | (-2,-1) | D. | ($\frac{1}{2}$,2) |
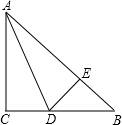 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.