题目内容
6.(1)填空:21-20=2( ),22-21=2( ),23-22=2( ),…(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立:
(3)计算:20+21+22+…+29.
分析 (1)根据乘方的运算法则计算即可;
(2)根据式子规律可得2n-2n-1=2n-1,然后利用提公因式2n-1可以证明这个等式成立;
(3)设题中的表达式为a,再根据同底数幂的乘法得出2a的表达式,相减即可.
解答 解:(1)21-20=2-1=20,22-21=4-2=21,23-22=8-4=22,
故答案为:0,1,2;
(2)第n个等式为:2n-2n-1=2n-1,
∵左边=2n-2n-1=2n-1(2-1)=2n-1,
右边=2n-1,
∴左边=右边,
∴2n-2n-1=2n-1;
(3)设a=2°+21+22+23+…+28+29.①
则2a=21+22+23+…+28+29+210②
由②-①得:a=210-1,
∴20+21+22+23+…+28+29=210-1.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:2n-2n-1=2n-1成立.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
20.方程x2=x的解是( )
| A. | x=1 | B. | x1=-1,x2=1 | C. | x1=0,x2=1 | D. | x=0 |
17. 若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )
若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )
 若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )
若有理数m,n在数轴上的位置如图所示,下列各式正确的是( )| A. | -m<0 | B. | m+n>0 | C. | -n<|m| | D. | mn>0 |
16.若a,b,为等腰△ABC的两边,且满足|a-4|+$\sqrt{b-2}$=0,则△ABC的周长为( )
| A. | 8 | B. | 6 | C. | 8或10 | D. | 10 |
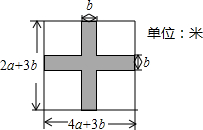 如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.
如图,在某住房小区的建设中,为了提高业主的宜居环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.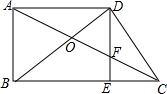 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.