题目内容
11.在△ABC中,AB=5,BC=12,AC=13,则AC边上的高是$\frac{60}{13}$.分析 先根据勾股定理的逆定理判定△ABC为直角三角形,再利用面积法进行求解.
解答 解:∵在△ABC中,AB=5,BC=12,AC=13,
∴AB2+BC2=52+122=132=AC2,
∴△ABC为直角三角形,且∠B=90°,
∵直角边为AB,BC,设斜边AC上的高为h,
根据三角形的面积有:$\frac{1}{2}$×5×12=$\frac{1}{2}$×13h,
解得h=$\frac{60}{13}$,
故答案为$\frac{60}{13}$.
点评 本题考查了勾股定理的逆定理和直角三角形的面积的综合应用.先判定△ABC为直角三角形是解题的关键.

练习册系列答案
相关题目
20.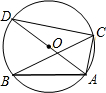 如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
 如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )
如图,△ABC内接于圆O,AD是圆O的直径,∠ABC=30°,则∠CAD的度数等于( )| A. | 45° | B. | 50° | C. | 55° | D. | 60° |
 已知如图,△ABC中,∠C=90°,AB=10,BC=6,
已知如图,△ABC中,∠C=90°,AB=10,BC=6,