题目内容
5.有甲、乙两个不透明的口袋,甲口袋中装有3个小球,上面分别标有数字1,2,3,乙口袋中装有2个小球,上面分别标有数字4,5,每个小球除数字不同外其余均相同,现从甲口袋中随机摸出一个小球,再从乙口袋中随机摸出一个小球.请用画树状图(或列表)的方法,求两次摸出的小球上的数字之和能被3整除的概率.分析 画树状图展示所有6种等可能的结果数,再找出两次摸出的小球上的数字之和能被3整除的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有6种等可能的结果数,其中两次摸出的小球上的数字之和能被3整除的结果数为2,
所以两次摸出的小球上的数字之和能被3整除的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
9.下列运算正确的是( )
| A. | (x3)2=x5 | B. | (-x)5=-x5 | C. | x3•x2=x6 | D. | 3x2+2x3=5x5 |
10. 已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
 已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )
已知:如图,在⊙O中,OA⊥BC,∠AOB=70°,则∠ADC的度数为( )| A. | 30° | B. | 35° | C. | 45° | D. | 70° |
7.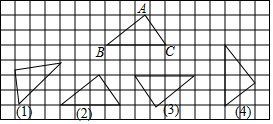 图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
 图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
17.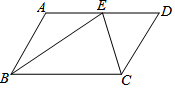 如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )
如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )
 如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )
如图,在平行四边形ABCD中,AD=10 cm,CD=6 cm,E为AD上任意的一点,且BE=BC,CE=CD,则DE的长度是( )| A. | 3 cm | B. | 3.5 cm | C. | 3.6 cm | D. | 4 cm |
14.下列命题是真命题的是( )
| A. | 菱形的对角线互相平分 | |
| B. | 一组对边平行,一组对边相等的四边形是平行四边形 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线相等的四边形是矩形 |