题目内容
 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为考点:角平分线的性质,等腰直角三角形
专题:
分析:过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得点D到AC的距离也等于DE,然后利用△ABC的面积列方程求出DE,再判断出△ADE是等腰直角三角形,根据等腰直角三角形的性质求出AE,再求出BE,然后利用勾股定理列式计算即可得解.
解答: 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵AD平分∠BAC,
∴点D到AC的距离也等于DE,
∴S△ABC=
×3•DE+
×4•DE=
×3×4,
解得DE=
,
∵AD平分∠BAC,∠BAC=90°,
∴∠DAE=45°,
∴△ADE是等腰直角三角形,
∴AE=DE=
,
∴BE=3-
=
,
在Rt△BDE中,BD=
=
=
.
故答案为:
.
 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,∵AD平分∠BAC,
∴点D到AC的距离也等于DE,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得DE=
| 12 |
| 7 |
∵AD平分∠BAC,∠BAC=90°,
∴∠DAE=45°,
∴△ADE是等腰直角三角形,
∴AE=DE=
| 12 |
| 7 |
∴BE=3-
| 12 |
| 7 |
| 9 |
| 7 |
在Rt△BDE中,BD=
| DE2+BE2 |
(
|
| 15 |
| 7 |
故答案为:
| 15 |
| 7 |
点评:本题考查了角平分线上的点到角的两边距离相等的性质,等腰直角三角形的判定与性质,勾股定理,熟记各性质并作辅助线构造出等腰直角三角形是解题的关键.

练习册系列答案
相关题目
在数轴上与表示-3的点的距离等于5的点所表示的数是( )
| A、-8 | B、2 |
| C、8和-2 | D、-8和2 |
一个等腰三角形的两条边长分别为7,11,则这个等腰三角形的周长为( )
| A、25 | B、29 |
| C、18 | D、25或29 |
观察下列一组数的排列:1,2,3,4,3,2,1,2,3,4,3,2,1,…,那么第2014个数是( )
| A、1 | B、2 | C、3 | D、4 |
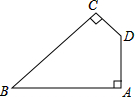 如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积.
如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积. 如图所示,将图沿虚线折起来,得到一个正方体,那么“我”的对面是
如图所示,将图沿虚线折起来,得到一个正方体,那么“我”的对面是