题目内容
 C为线段AB上的点,DA、EB、CF均垂直于AB,且DA=CB,EB=AC,CF=AB.求证:∠AFD=∠BFE.
C为线段AB上的点,DA、EB、CF均垂直于AB,且DA=CB,EB=AC,CF=AB.求证:∠AFD=∠BFE.考点:全等三角形的判定与性质
专题:证明题
分析:连接BD,AE,易证Rt△DAB≌Rt△BCF和Rt△EBA≌Rt△ACF,即可得△BDF和△AEF为等腰直角三角形,即可求得∠AFE=∠BFD,即可解题.
解答:证明:连接BD,AE,

∵在Rt△DAB和Rt△BCF中,
,
∴Rt△DAB≌Rt△BCF,(HL)
∴BD=BF,∠DBA=∠BFC,
∵∠BFC+∠FBA=90°,
∴∠DBA+∠FBA=90°,即BD⊥BF,
∴△BDF为等腰直角三角形,∠BFD=45°,
∵在Rt△EBA和Rt△ACF中,
,
∴Rt△EBA≌Rt△ACF,(HL)
∴AE=AF,∠EAB=∠AFC,
∵∠FAB+∠AFC=90°,
∴∠EAB+∠FAB=90°,即AE⊥AF,
∴△AEF是等腰直角三角形,∠AFE=45°
∴∠AFE=∠BFD,
即∠BFD-∠EFD=∠AFE-∠EFD
∴∠AFD=∠BFE.

∵在Rt△DAB和Rt△BCF中,
|
∴Rt△DAB≌Rt△BCF,(HL)
∴BD=BF,∠DBA=∠BFC,
∵∠BFC+∠FBA=90°,
∴∠DBA+∠FBA=90°,即BD⊥BF,
∴△BDF为等腰直角三角形,∠BFD=45°,
∵在Rt△EBA和Rt△ACF中,
|
∴Rt△EBA≌Rt△ACF,(HL)
∴AE=AF,∠EAB=∠AFC,
∵∠FAB+∠AFC=90°,
∴∠EAB+∠FAB=90°,即AE⊥AF,
∴△AEF是等腰直角三角形,∠AFE=45°
∴∠AFE=∠BFD,
即∠BFD-∠EFD=∠AFE-∠EFD
∴∠AFD=∠BFE.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证Rt△DAB≌Rt△BCF和Rt△EBA≌Rt△ACF是解题的关键.

练习册系列答案
相关题目
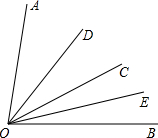 如图,已知∠DOC=25°,∠EOC=15°,OD平分∠AOC,OE平分∠BOC,求∠AOC、∠BOC、∠AOB的度数.
如图,已知∠DOC=25°,∠EOC=15°,OD平分∠AOC,OE平分∠BOC,求∠AOC、∠BOC、∠AOB的度数.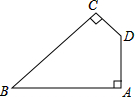 如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积.
如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积. 如图所示,将图沿虚线折起来,得到一个正方体,那么“我”的对面是
如图所示,将图沿虚线折起来,得到一个正方体,那么“我”的对面是