题目内容
10. 如图,AB=4,点O是线段AB上的点,点C,D分别是线段OA,OB的中点.
如图,AB=4,点O是线段AB上的点,点C,D分别是线段OA,OB的中点.(1)则CD=2(直线写出答案);
(2)若AB=m,点O是线段AB上的点,点C、D分别是线段OA、OB的中点,则CD=$\frac{m}{2}$(说明理由);
(3)若点O运动到AB的延长线上,(2)中的结论是否还成立,画出图形分析,并说明理由.
分析 (1)根据中点的定义,将CO和OD表示出来,相加即可得出结论;
(2)根据中点的定义,将CO和OD表示出来,相加即可得出结论;
(3)若点O运动到AB的延长线上,可得知CD=CO-DO,由中点的定义,将CO和DO表示出来,相减即可得出结论.
解答 解:(1)CD=CO+OD=$\frac{AO}{2}$+$\frac{BO}{2}$=$\frac{AB}{2}$=4÷2=2,
故答案为:2.
(2)∵点O是线段AB上的点,点C、D分别是线段OA、OB的中点,且AB=m,
∴CD=CO+OD=$\frac{AO}{2}$+$\frac{BO}{2}$=$\frac{AB}{2}$=$\frac{m}{2}$,
故答案为:$\frac{m}{2}$.
(3)若点O运动到AB的延长线上,(2)结论仍然成立,画图如下,
CO=$\frac{AB+BO}{2}$,DO=$\frac{BO}{2}$,
CD=CO-DO=$\frac{AB}{2}$=$\frac{m}{2}$.
故若点O运动到AB的延长线上,(2)中的结论成立.
点评 本题考查两点间的距离,解题的关键是根据中点的定义,将CO和OD表示出来,再依据点O的位置决定是相加还是相减.

练习册系列答案
相关题目
15.下列命题中,是真命题的是( )
| A. | 同位角相等 | B. | 全等的两个三角形一定是轴对称 | ||
| C. | 不相等的角不是内错角 | D. | 同旁内角互补,两直线平行 |
20. 如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )
如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )
 如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )
如图,点A在由函数y=(-1)2(x-3n)(x-3n-3)(3n≤x<3n+3,为自然数)的图象组成的平滑曲线上,点B在x轴上,且AB⊥x轴,若点B从原点O出发,沿x轴向右以每秒1个单位长的速度运动,则第2016秒时,点A的坐标是( )| A. | (2016,0) | B. | (2016,2) | C. | (2015,0) | D. | (2016,-2) |
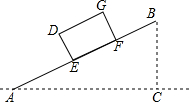 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部B处的高BC为8m,A、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部B处的高BC为8m,A、C在同一水平地面上.