题目内容
11．已知关于x的一元二次方程x2+x-k=0的一个根是x=1，则另一个根是-2．分析 通过根与系数的关系x1+x2=-p求得方程的另一个根．
解答 解：设关于x的一元二次方程x2+x-k=0的另一个根为x2，
则依题意得：1+x2=-1，
解得x2=-2．
故答案是：-2．
点评 本题考查了根与系数的关系．若二次项系数为1，常用以下关系：x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1x2=q，反过来可得p=-（x1+x2），q=x1x2，前者是已知系数确定根的相关问题，后者是已知两根确定方程中未知系数．
练习册系列答案
阅读快车系列答案
相关题目
6．
如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，则下列比值：$\frac{AC}{AB}$，$\frac{BC}{AB}$，$\frac{CD}{AC}$，$\frac{BD}{BC}$，其中可以表示cosB的有（ ）
如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，则下列比值：$\frac{AC}{AB}$，$\frac{BC}{AB}$，$\frac{CD}{AC}$，$\frac{BD}{BC}$，其中可以表示cosB的有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
16．某机械厂七月份生产零件50万个，计划八、九月份共生产零件146万个，设八、九月份平均每月的增长率为x，那么x满足的方程是（ ）
| A． | 50（1+x）2=146 | B． | 50+50（1+x）+50（1+x）2=146 | ||
| C． | 50（1+x）+50（1+x）2=146 | D． | 50+50（1+x）+50（1+2x）=146 |
3．老师让同学们举一个y是x的函数的例子，同学们分别用表格、图象、函数表达式列举了如下4个x、y之间的关系：
其中y一定是x的函数的是④．（填写所有正确的序号）
①
| ② | ||||||||||
| ③ y=kx+b | ④ y=|x| |
20．
如图，点A在由函数y=（-1）2（x-3n）（x-3n-3）（3n≤x＜3n+3，为自然数）的图象组成的平滑曲线上，点B在x轴上，且AB⊥x轴，若点B从原点O出发，沿x轴向右以每秒1个单位长的速度运动，则第2016秒时，点A的坐标是（ ）
如图，点A在由函数y=（-1）2（x-3n）（x-3n-3）（3n≤x＜3n+3，为自然数）的图象组成的平滑曲线上，点B在x轴上，且AB⊥x轴，若点B从原点O出发，沿x轴向右以每秒1个单位长的速度运动，则第2016秒时，点A的坐标是（ ）| A． | （2016，0） | B． | （2016，2） | C． | （2015，0） | D． | （2016，-2） |
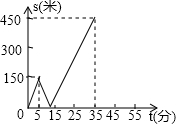甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走．设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数函数图象的一部分如图所示．